Явища переносу

Явища переносу (дифузія, теплопровідність, внутрішнє тертя) полягають у виникненні напрямленого переносу в газах маси (дифузія), внутрішньої енергії (теплопровідність) та імпульсу направленого руху відповідно.

Явища переносу виникають при просторовій неоднорідності концентрації n, температури Т і швидкості напрямленого руху частинок u. Вирівнювання значень n, T, u в об'ємі відбувається за рахунок теплового руху частинок, що характеризується середньою швидкістю V.

1. Експериментально визначено, що при одновимірній дифузіїоднорідного газу, число частинок N, що переносяться за час dt через елементарний поперечний переріз S визначається законом Фіка

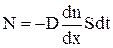, (1)

де D¾коефіцієнт дифузії.

Якщо ліву і праву частини (1) домножити на масу частинки газу, то одержимо вираз для маси газу m, що переноситься за час dt через елементарний поперечний переріз S при одновимірній дифузії.

, (2)

2. Експериментальновизначено, що для ідеального газу в одновимірному стаціонарному випадку кількість тепла dq, що переноситься в напрямку ОХ нормально до площадки dS за час dt визначається законом Фур'є:

, (3)

де c¾коефіцієнттеплопровідності.

3. Силавнутрішнього тертя F, що діє на площадку S поверхні шару ^ Ох при просторовій неоднорідності швидкості напрямленого руху 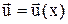^ OX визначається законом Ньютона

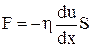, (4)

де h¾коефіцієнтв'язкості.

6.13. Дифузія

Для визначення коефіцієнта дифузіїD, розглянемо одновимірний рух частинок, як показано на Мал.54. Нехай концентрація частинок є функцією координати х: n=f(x), а число частинок, що рухаються в напрямкові осі ОХ дорівнює

. (1)

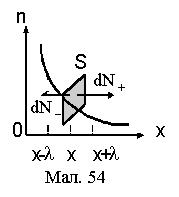В додатному напрямку ОХ через S ^ ОХ, що має координату х, за 1с пройде

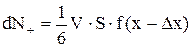(2)

частинок, де величина Dх задає координату точки, починаючи з якої частинки без співударяння пройдуть через S. Такою величиною є середня довжина вільного пробігу Dх = l. Аналогічно в протилежному напрямкові пройде

(3)

частинок, де також Dх = l. З визначення похідної

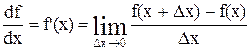(4)

для достатньо малих Dх, що задовольняють певній точності обчислення похідної, можна записати

(5)

і звідси

, (6)

або в загальному виді значення функції в точці х±Dх можна записати через значення функції та її похідної у точці х таким чином

, (7)

причому

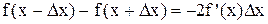. (8)

Зважаючи на останній вираз можна записати

(9)

(10)

Різниця

(11)

і зважаючи на те, що , запишемо

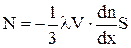. (12)

Порівнюючи одержаний вираз для N з експериментальним N= -D S, маємо для коефіцієнта дифузії значення

. (13)

Для повітря при нормальних умовах .

6.14. Теплопровідність

Якщо дві частини середовища, або два різні середовища, що контактують між собою, мають різні температури, то між ними виникає тепловий потік від тіла з більшою температурою до тіла з меншою температурою.

Таблиця 2. Коефіцієнт теплопровідності c деяких речовин

Речовина	χ,	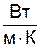Речовина	χ,	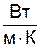Речовина	χ,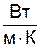
Срібло Мідь Золото Алюміній Латунь Платина Олово Сірий чавун Бронза Сталь Свинець Ртуть	47 - 58 8,2	Накип Мармур Лід (0°С) Пісчаник Фарфор Скло (кварц.) Бетон Скло Цегла Вода Азбест Кожа	2,8 2,23 1,4 1,36 0,7—1,2 0,7 ~ 0,7 0.58 0,4—0,8 0,15	Дерево Пробка Скловата Войлок Шамот Пінопласт Сухий пісок Азот Пар Повітря Перо Вакуум	0,1 — 0.2 0,05 0,05 0,046 0,04 0,04 0,325 0,0236 0,024 0,034 0.02 0,00

Для визначення коефіцієнта теплопровідності , розглянемо одновимірний рух частинок, як показано на Мал.55. Концентрація частинок, що рухаються вздовж осі ОХ ¾ 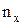, температура Т є функція х і вона дорівнює T= f(x). Енергія частинки .

Покладемо, що концентрація частинок є сталою. В зустрічних напрямках по осі ОХ через поверхню S ^ ОХ, що має координату х, за час dt пройде

частинок. Частинки, що переходять S у додатному напрямку ОХ переносять енергію

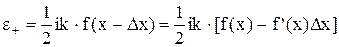
а частинки, що рухаються назустріч

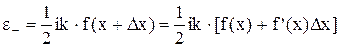
де Dх задає координату точок до поверхні S, починаючи з яких, частинки без співударяння пройдуть через S. Такими є точки x±Dx, де Dх = l.

Теплова енергія, що переноситься частинками в зустрічних напрямках осі ОХ дорівнює

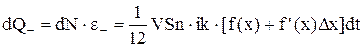
Результуюча теплова енергія, що переноситься в напрямкові зменшення температури через поверхню S

Величина ikn/2 = с_Vr[1], де с_V ¾ питома теплоємність газу при сталому об'ємі, а r ¾ його густина. Тепер

Порівнюючи одержаний вираз із формулою Фур'є ,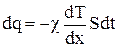

маємо

.

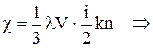
Коефіцієнт теплопровідності можна записати через коефіцієнт дифузії D

.

Для повітря, як ідеального газу, при нормальних умовах .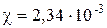

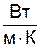6.15. Внутрішнє тертя

Явище внутрішнього тертя (в'язкості) полягає у вирівнюванні швидкості напрямленого руху суміжних шарів газу або рідини, що рухаються паралельно один одному з різними швидкостями u, шляхом теплового перенесення частинками направленого імпульсу з одного шару в інший. Таке явище можна описати силами внутрішнього тертя, що виникають між шарами.

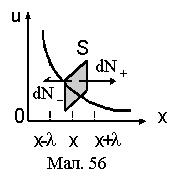
Для визначення коефіцієнта в'язкості h, розглянемо одновимірний рух частинок, як показано на Мал.56. Концентрація частинок, що рухаються вздовж осі ОХ ¾ n, а швидкість напрямленого руху u є функція х і вона дорівнює u=f(x).

В зустрічних напрямках по осі ОХ через плоску поверхню S ^ ОХ, що має координату х, за час dt пройде

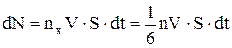
частинок. Ми допустили, що концентрація частинок стала величина i 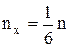. Частинки, що переходять S у додатному напрямку ОХ мають імпульс

р ₊ = mu(x - Dx) = mf(x - Dx),

а частинки, що рухаються назустріч

p _- = mu(x + Dx) = mf(x + Dx).

Значення швидкості u потрібно взяти в тій точці, починаючи з якої частинки без співударяння пройдуть через S. Такими є точки x±Dx із Dх = l. Імпульс, що переноситься частинками в зустрічних напрямках осі ОХ дорівнює

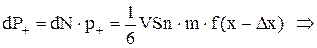
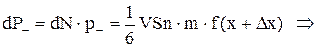
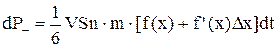
Імпульс, що переноситься в напрямкові зменшення швидкості u

За другим законом Ньютона де F сила, що діє на поверхню S

,

де r = mn ¾ густина газу. Порівнюючи одержаний вираз із законом Ньютона F = - h S, знайдемо коефіцієнт в'язкості у вигляді

.

Коефіцієнт в'язкості h можна виразити через коефіцієнт дифузії . Величина 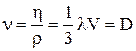називається кінематичною в'язкістю, яка чисельно дорівнює коефіцієнтові дифузії. Між коефіцієнтами переносу D, та 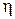можна встановити взаємозв'язок:

.

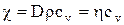Для повітря при нормальних умовах 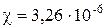Па×с.

6.16. Контрольні питання

1. Визначіть основні положення молекулярної фізики?

2. Що є структурними частинками речовини?

3. Який статистичний розподіл частинок за напрямком руху?

4. У чому полягає статистичний метод дослідження речовини?

5. Які положення лежать в основі молекулярно-кінетичної теорії?

6. Як визначається імовірність деякого стану речовини?

7. Як визначається імовірність А при N вимірюваннях?

8. Як визначається густина ймовірності?

9. Як визначається умова нормування ймовірності дискретних станів?

10. Як визначається умова нормування ймовірності при неперервній зміні стану?

11. Що являють собою флуктуації?

12. Що визначає дисперсія флуктуації?

13. Який фізичний зміст флуктуацій термодинамічних величин?

14. Як визначається ідеальний газ?

15. Поясніть, що являють собою молекула та атом.

16. Що лежить в основі атомної одиниці маси?

17. Яка величина атомної одиниці маси?

18. Визначіть поняття моля та молярної маси речовини.

19. Дайте визначення тиску.

20. Що визначає температура?

21. Які існують шкали температур?

22. Визначте нормальні умови газу.

23. Яке визначення ступенів свободи частинки?

24. Як визначаються поступальні, обертові та коливальні ступені свободи?

25. Яке визначення ступенів свободи системи з N жорстко зв'язаних атомів?

26. Що таке зв'язки? Як вони впливають на кількість ступенів свободи?

27. Поясніть теорему Больцмана про рівнорозподіл енергії.

28. Чому дорівнює поступальна, обертова та коливальна енергія частинки?

29. Як розрахувати енергію молекули з N атомами?

30. Як розрахувати енергію ідеального газу з N структурними частинками?

31. Як розрахувати енергію ідеального газу через тиск та об'єм?

32. Обчисліть тиск газу за молекулярно кінетичною теорією.

33. Визначте ефективний діаметр частинок.

34. Визначте ефективний газокінетичний поперечний переріз для газу.

35. В чому полягає розподіл частинок ідеального газу за напрямком руху?

36. Розрахуйте число зіткнень частинки ідеального газу за одиницю часу.

37. Розрахуйте середню довжину вільного пробігу частинки ідеального газу.

38. Опишіть розподіл Максвелла для частинок ідеального газу за швидкостями.

39. Опишіть густину розподілу Максвелла.

40. Опишіть розподіл Максвелла для скінчених малих величин DV.

41. Визначте положення максимуму густини розподілу Максвелла.

42. Розрахуйте найбільш імовірну швидкість частинки ідеального газу.

43. Розрахуйте середню арифметичну швидкість частинки ідеального газу.

44. Розрахуйте середню квадратичн швидкість частинки ідеального газу.

45. Опишіть дослід Б. Ламмерта по визначенню середньої теплової швидкості.

46. Виведіть барометричну формулу.

47. Визначте розподіл Больцмана

48. Визначте розподіл Максвелла - Больцмана

49. Опишіть явища переносу (дифузію, теплопровідність, внутрішнє тертя)

50. Опишіть закон дифузіїФіка.

51. Опишіть закон теплопровідності Фур'є.

52. Опишіть закон внутрішнього тертя Ньютона.

53. Виведіть вираз для коефіцієнта дифузіїD.

54. Виведіть вираз для коефіцієнта теплопровідності k.

55. Виведіть вираз для коефіцієнта в'язкості h.

56. Виведіть формули для зв'язку між коефіцієнтами D, k, h.

[1] Послідовні обчислення дають: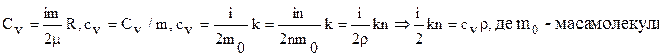

Дата добавления: 2015-10-28