THE CRASH OF '87

That big risk came home to roost on Monday, October 19, 1987. I was out of town at the time. My wife and I had decided to take a three-day weekend to hike through foliage and stay in an upstate inn. The previous week had been bad in the stock market, and there was a pronounced nervousness. On Friday morning, October 16, Deborah suggested that we sell our stock. I wanted to get away early to beat traffic, and I uttered the famous last words, "Let's talk about it on Tuesday."

I'm not going to talk about the complex causes of the crash, nor the frightening events of Tuesday, when the market almost failed completely. At the time, people focused on portfolio insurance, program trading, and lack of circuit breakers-none of which appear to have been significant factors, in retrospect. Underpriced put options, which led people to invest in the stock market without assuming risk, were vastly more important.

What is truly amazing is the sudden paradigm shift in all financial markets. From the first exchange-traded options in 1973 until October 16, 1987, all options on the same underlying for the same expiry date had been priced assuming the same-size move. If prices deviated a little bit, dealers came in and took advantage of the difference until it disappeared. This was true not just in the stock market; it held for commodity, interest rate, and foreign exchange options as well.

As soon as options resumed anything like normal trading-certainly by Thursday, October 22-that assumption had disappeared without a trace. It happened in all markets simultaneously, without comment or explanation. Now if the $20 put traded on one volatility assumption and the $25 call traded on a different one, nobody rushed in to take advantage of the "discrepancy." No one talked about it, but portfolios that had been treated as riskless a week earlier were assigned significant amounts of risk capital.

To see what I mean, let's go back to the example of betting on the World Series. Pre-1987, the assumption that you could get 2:1 odds betting on the Braves meant the seven-game bet was worth $225. The same assumption means a $100 bet on the Yankees to win the series should pay off $135. To match this payoff, you bet $40 on the Yankees to win game 5. If they win game 5, you bet $30 on them in game 6; otherwise, you bet $60. If the Yankees win games 5 and 6, you have $135. If they lose games 5 and 6, you have $0. If they split, you have $90, which you bet on the Yankees to win in game 7, collecting $135 if they do and nothing if they don't (see Figure 4.3).

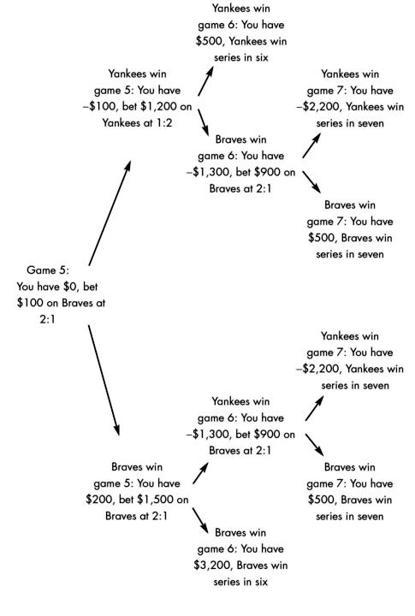
Suppose that the seven-game bet paid $225, but betting on the Yankees to win the World Series paid $180 instead of $135. Precrash, everyone treated this as an opportunity. If the seven-game bet was priced correctly, betting on the Yankees to win the series was a great bet. If the Yankees series bet was correct, the seven-game bet should pay only $201, so getting $225 was good as well. To take maximum advantage, let's bet $1,500 on the Yankees to win, getting $2,700 if we are right, and $1,200 on the series to go seven games, also getting $2,700 if we are right. If we win one of the two bets, we break even. If the Yankees win in seven, we make $2,700. The only risk is if the Braves win in six, in which case we lose $2,700. But we don't want any risk. We're going to put together a hedging strategy to make sure we profit at least $500 whatever happens (see Figure 4.4).

Our hedge betting produces a profit of $3,200 when the Braves win in six. We lose both of our original bets, costing us $2,700, but our net profit in this case is $500. If the Yankees win in seven, we lose $2,200 from our hedge but win both our original bets, for a profit of $2,700. Again, we have a net profit of $500. In all other cases, we make $500 from our hedge and break even on the original bets. We have a riskless profit, an arbitrage. More important, we don't care what the odds are on Yankees-Braves games. We might change our initial bets and our hedging strategy as a result, but there's always an arbitrage profit when (a) you can bet on the Yankees to win the series at 0.8:1, (b) you can bet on a seven-game series at 1.25:1, and (c) you can bet on individual Yankees-Braves games all at the same odds. It was (c) that bit the market.

Figure 4.3

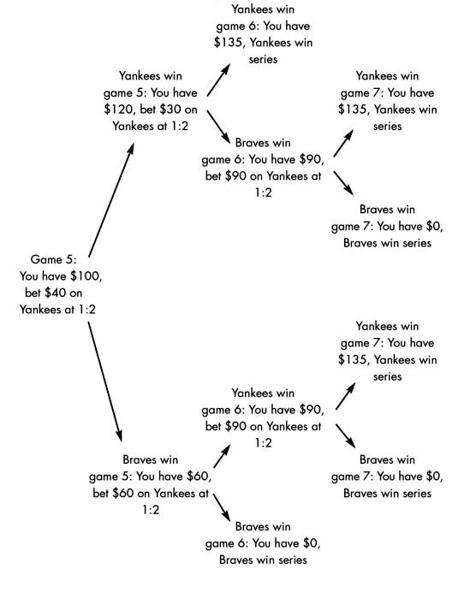
Figure 4.4

Of course, once you find something like this, you bet more and more, borrowing whatever money you can. That drives the profits down; instead of betting $2,700 to make $500, you're betting $5,400 to make $250, then $10,800 to make $125. The prices of the seven-game bet and the Yankees series bet get driven closer to theoretical parity.

Suppose you had been doing this for five years, doubling your bets for half the profit every year, until 1987. You've got to game 6 with the series tied 3-3, meaning your hedge has lost $1,300. Adding the cost of your original bets, you are $4,000 out of pocket. You don't mind that, however, because you've already won the seven-game bet for $2,700, and if the Yankees win game 7, you have another $2,700 coming in. You go to place your $900 bet on the Braves, only to be told the odds are no longer 2:1. The entire Yankee pitching staff came down with the flu and the betting odds on the Braves have moved to 1:2. The best you can do is bet $1,800 on the Braves and take a $400 loss whoever wins. Only by this time, it's not a $400 loss when you expected to make $500, it's 32 times the loss ($12,800) when you expected to make 1/2 of the profit ($16).

The amazing thing was that as soon as this happened, the payouts snapped back to $180 and $225, and no one said anything about it being an arbitrage. Derivatives were gambles after all, and people got to work to monitor and manage the risk. The more accurate derivative pricing made the securities far more precise levers of financial control and ushered in a new era of financial engineering.

This is the closest thing to a miracle that I ever expect to see. The markets collapsed, completely and unexpectedly, but when the dust cleared, everything was rearranged in a stable formation. Imagine if an earthquake hit San Francisco and the Embarcadero floated into the bay to form a nice island with all the buildings intact-and the rest of the city slid around, but everything ended up in a convenient location. Then imagine no one talked about it; they just went about their business as if nothing had happened.

By the way, for people who want to go one more step in understanding financial math, there were two main quantitative solutions to the new derivative pricing problems. If we accept that it is correct to pay $180 for a $100 bet on the Yankees to win the series, and $225 for a bet that the series would go seven games, then we can explain things by assuming different odds for each game. In this case, if the Yankees are 2:1 favorites in games 5 and 6, but 1:3 underdogs in game 7 (perhaps the Braves' star pitcher will be ready for that one while the Yankees will have run out of rested starters). This is called local volatility because we know in advance the odds of every game, but they're not the same for all games.

The alternative is to assume that the game odds are partially random. We know the odds for game 5, but not for games 6 and 7. We might find that we have to place our bets at 3:1 or 1:1 for game 6we don't know in advance. This is called stochastic volatility. Local volatility preserves the riskless hedge; it's more complicated, but there is one. Stochastic volatility means that the derivative is no longer a derivative-its price does not depend only on the underlying; it can move up or down on its own account. There is no more riskless hedge.

Although both these models are used in different areas of finance, they tend to give opposite recommendations for hedging and strategy. This has led to fruitful research into the nature of risk and unlimited employment opportunities for quants. Volatility does change, but it is neither stochastic nor predictable. Basic theoretical breakthroughs are needed before we will understand its nature. The grand unification challenge in theoretical finance is to come up with a model that aligns the predictions of local volatility models, stochastic volatility models, and actual future price movements (at the moment, neither model is good at that).

Of course, there were casualties of the 1987 crash. Some of the chess, poker, bridge, and backgammon players in the options markets lost most of their money; a lot of others lost as well. One particular story of relevance to poker concerns Roger Low, one of the three best backgammon players of the 1970s, who had been recruited in options trading by Ron Rubin, whose exciting story will be told in detail in Chapter 7. Roger had hired another backgammon champion, Erik Seidel. Both Roger and Erik tapped out big-time in the crash. Erik switched to poker and became one of the top players. Roger got off the trading floor and opened the Parallax hedge fund. Bridge champion josh Parker also moved upstairs (that means he started trading large block orders over the telephone instead of smaller lots on the floor) and later joined the Gargoyle hedge fund with two other bridge champions. Mike Becker, also profiled in Chapter 7, struggled for a few years to help his traders survive, then moved to Florida to play tennis and golf. These were the three choices for games players in the 1990s and later: Move into more mainstream financial jobs, go back to making a living at games, or quit with the money you already made and do whatever you want. It's still helpful at many financial firms to have some serious games success on your resume, but it better be in the "hobbies and interests" section, and you have to make clear to most interviewers that you have put away childish things.

For financial quants, the revelation was that risk had a price. There was a stable, liquid, rational market for risk. Options weren't riskless, but they weren't incommutably dangerous, either. Finance was demonstrated to be gambling, which shook things up, but when the shaking stopped, it turned out to be possible to compute the odds. That made it a rational game that people could play with limited risk and reasonable odds of winning. That changed the world forever.

FLASHBACK

Дата добавления: 2015-10-26