
Читайте также:
|
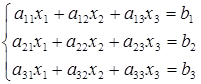
(6)
Составим матрицу системы из коэффициентов при неизвестных:
 .
.
Из неизвестных  ,
,  ,
,  и свободных членов составим матрицы – столбцы
и свободных членов составим матрицы – столбцы
 ;
; 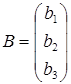 .
.
Тогда система (6) в матричной форме примет вид
 .
.
(7)
Чтобы найти матрицу  , умножим (7) на
, умножим (7) на  слева.
слева.
A 

ПРИМЕР 8.
 .
. 
Найти обратную матрицу  .
.
РЕШЕНИЕ.
1) Составляем и вычисляем определитель
 .
.
Определитель вычислен по правилу треугольника.
2) Транспонируем матрицу. Получаем
 .
.
3) Вычисляем алгебраические дополнения
 ;
;  ;
;  ;
; 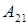 ;
;  ;
;  ;
;  ;
;  ;
; 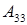 .
.
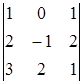 ;
; 
Вычисляем  . Вычеркиваем первую строку и второй столбец. Составляем определитель второго порядка из оставшихся элементов.
. Вычеркиваем первую строку и второй столбец. Составляем определитель второго порядка из оставшихся элементов.
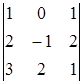 ;
;  .
.
Вычисляем  .
.
Аналогично вычисляем все остальные алгебраические дополнения:
 ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 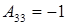 .
.
Составим обратную матрицу
A 
A 
Сделаем проверку

ПРИМЕР 9.
Решить систему матричным способом
 .
.
Из коэффициентов при неизвестных составим матрицу  :
:
 .
.
Из неизвестных составим матрицу – столбец:
 .
.
Из свободных членов составим матрицу – столбец:
 .
.
Тогда система запишется в виде
 .
.
Получили матричное уравнение. Умножаем обе части этого уравнения на  слева. Получаем:
слева. Получаем:
 .
.
Находим обратную матрицу:
 ;
;  ;
;
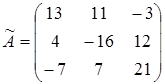 ;
; 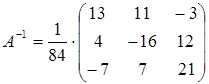 .
.
Умножая обратную матрицу на  , получаем матрицу
, получаем матрицу  .
.
 .
.
Отсюда получаем ответ:
 ;
;  ;
;  .
.
Сравните решение этой системы с решением метода Гаусса.
11. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
ОПРЕДЕЛЕНИЕ 1. Вектором называют направленный отрезок в пространстве или на плоскости, который можно передвигать параллельно самому себе. Один конец называется началом (точка  ), а другой конец (точка
), а другой конец (точка  ) – концом вектора
) – концом вектора  .
.




вектор  вектор
вектор 


Вектор  характеризуется длиной (или модулем
характеризуется длиной (или модулем  ), которая равна длине отрезка
), которая равна длине отрезка  , и направлением от
, и направлением от  к
к  .
.
ОПРЕДЕЛЕНИЕ 2. Два вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых ( ).
).
ОПРЕДЕЛЕНИЕ 3. Векторы называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях.
Определим линейные операции над векторами. К таким операциям относятся сложение (вычитание) векторов и умножение вектора на число.
Сложение и вычитание векторов можно выполнить по правилу треугольника (рис. 1а) или по правилу параллелограмма (рис. 1б).
 | |||||
 | |||||
 | |||||



 |





Рис. 1а Рис. 1б
ОПРЕДЕЛЕНИЕ 4. Произведением вектора  на число
на число  называют такой вектор
называют такой вектор 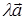 , длина которого равна
, длина которого равна  , а направление совпадает с направлением
, а направление совпадает с направлением  , если
, если 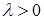 , и противоположно
, и противоположно  , если
, если  .
.
Если  , то вектор
, то вектор  называется противоположным к
называется противоположным к  (рис. 2).
(рис. 2).
 | |||||
 | |||||
 | |||||


( )
)
Рис. 2
ОПРЕДЕЛЕНИЕ 5. Множество всех векторов пространства с введенными на нем операциями сложения и умножения на число образует векторное пространство.
Определим понятие базиса и координат вектора в данном базисе.
ОПЕРЕДЕЛЕНИЕ 6. Система векторов  ,
,  ,
,  , …,
, …,  называется линейно зависимой, если существуют числа
называется линейно зависимой, если существуют числа  ,
,  , …
, …  , такие, что хотя бы одно из них отлично от нуля и
, такие, что хотя бы одно из них отлично от нуля и
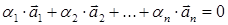
(8)
Если система линейно независима, то в (8) все  . Пусть для определенности коэффициент
. Пусть для определенности коэффициент 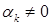 , тогда из равенства (8) можно найти
, тогда из равенства (8) можно найти
 .
.
Итак, для линейно зависимой системы векторов  ,
,  ,
,  , …,
, …,  любой вектор можно представить как линейную комбинацию остальных (
любой вектор можно представить как линейную комбинацию остальных ( ) векторов. Для линейно независимой системы векторов такое представление невозможно.
) векторов. Для линейно независимой системы векторов такое представление невозможно.
ОПРЕДЕЛЕНИЕ 7. Совокупность линейно независимых векторов  ,
,  , …,
, …, 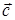 , взятых в определенном порядке, образует базис пространства, и обозначается базис
, взятых в определенном порядке, образует базис пространства, и обозначается базис  .
.
На плоскости (в  ) базис образует два линейно независимых вектора, в трехмерном пространстве (в
) базис образует два линейно независимых вектора, в трехмерном пространстве (в  ) – три линейно независимых вектора и в пространстве
) – три линейно независимых вектора и в пространстве  –
–  линейно независимых векторов.
линейно независимых векторов.

 Два коллинеарных вектора
Два коллинеарных вектора  и
и  являются зависимыми, так как
являются зависимыми, так как  . Поэтому на плоскости два любых неколлинеарных вектора образуют базис. Аналогично, три любых некомпланарных вектора образуют базис трехмерного пространства
. Поэтому на плоскости два любых неколлинеарных вектора образуют базис. Аналогично, три любых некомпланарных вектора образуют базис трехмерного пространства  .
.







Базис в 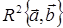 Базис в
Базис в 
ОПРЕДЕЛЕНИЕ 8. Любой вектор  в пространстве
в пространстве  единственным образом определяется в виде суммы:
единственным образом определяется в виде суммы:
 ,
,
(9)
где числа 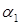 ,
,  ,
,  называются координатами вектора
называются координатами вектора  в данном базисе.
в данном базисе.
Равенство (9) представляет разложение вектора  по базису
по базису  в трехмерном пространстве (в
в трехмерном пространстве (в  ). На плоскости (в
). На плоскости (в  ) вектор
) вектор  имеет разложение по базису
имеет разложение по базису  :
:
 .
.
Замечание. Записи  и
и  означают одно и то же: вектор
означают одно и то же: вектор  имеет координаты
имеет координаты 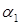 ,
,  ,
,  в данном базисе
в данном базисе  .
.
Необходимым и достаточным условием линейной независимости трех векторов 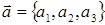 ,
,  и
и  является условие:
является условие:
 .
.
ПРИМЕР 10. Найти разложение вектора  по векторам
по векторам  ,
, 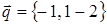 и
и  .
.
РЕШЕНИЕ. Проверим, являются ли векторы  ,
,  ,
,  линейно независимыми, то есть образуют ли они базис. Для этого вычислим определитель третьего порядка, составленный из координат векторов
линейно независимыми, то есть образуют ли они базис. Для этого вычислим определитель третьего порядка, составленный из координат векторов  ,
,  ,
,  по методу треугольника:
по методу треугольника:
 ,
,
то есть векторы  ,
,  ,
,  являются базисом, тогда
являются базисом, тогда  , где
, где 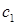 ,
,  ,
,  – неизвестные координаты вектора
– неизвестные координаты вектора 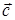 в базисе
в базисе  ,
,  ,
,  . Составим систему:
. Составим систему:
 .
.
Решаем методом Крамера:
 ;
;  ;
;
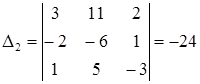 ;
;  .
.
 ,
, 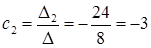 ,
,  .
.
Следовательно,  или
или 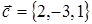 .
.
Линейные операции над векторами сводятся к линейным операциям над координатами этих векторов по следующим правилам:
1) Координаты алгебраической суммы векторов 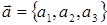 и
и  равны суммам соответствующих координат:
равны суммам соответствующих координат:

(10)
2) Координаты произведения вектора  на число
на число  равны произведениям координат
равны произведениям координат  на
на  :
:

(11)
Самым удобным является базис, состоящий из единичных взаимно перпендикулярных векторов.
В трехмерном пространстве с декартовыми прямоугольными координатами такой базис составляют векторы 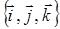 (рис. 3б), на плоскости –
(рис. 3б), на плоскости –  (рис. 3а).
(рис. 3а).





















 0
0 
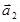




 0
0 


Рис. 3а Рис. 3б
Тогда координаты произвольного вектора  являются проекциями этого вектора на соответствующие координатные оси, и разложение вектора по базису
являются проекциями этого вектора на соответствующие координатные оси, и разложение вектора по базису 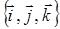 имеет вид
имеет вид
 или
или 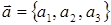
(12)
Такой базис называют декартов базис. В этом базисе справедливы следующие теоремы и формулы.
ТЕОРЕМА 1. Если известны координаты точек  и
и  , то координаты вектора
, то координаты вектора  находятся по формулам
находятся по формулам
 ,
,  ,
,  .
.
(13)
ПРИМЕР 11. Пусть даны две точки 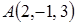 и
и  . Найти координаты
. Найти координаты  и
и  .
.
РЕШЕНИЕ.  и
и  – находим по формуле (13).
– находим по формуле (13).
Итак, если известны координаты начала и конца вектора, то для отыскания координат самого вектора нужно из координат конца вычесть соответствующие координаты начала.
ТЕОРЕМА 2. Если векторы  и
и  коллинеарны, то их координаты пропорциональны, то есть
коллинеарны, то их координаты пропорциональны, то есть
 ,
,  ;
;
 .
.
(14)
ОПРЕДЕЛЕНИЕ 9. Скалярным произведением векторов  и
и  (обозначается
(обозначается  ) называется число, равное произведению длин этих векторов на косинус угла между ними:
) называется число, равное произведению длин этих векторов на косинус угла между ними:
 .
.
(15)
ТЕОРЕМА 3. Скалярное произведение векторов  и
и  , заданных своими координатами, вычисляется по формуле
, заданных своими координатами, вычисляется по формуле

(16)
Скалярное произведение применяется в геометрии и механике:
1. Косинус угла между векторами  и
и  находится по формуле
находится по формуле







(17)
2. Проекция вектора  на вектор
на вектор  :
:
 .
.
(18)
3. Если два вектора  и
и  перпендикулярны, то
перпендикулярны, то 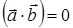 , то есть
, то есть
 ,
,
(19)
– условие перпендикулярности двух векторов.
4. Если вектор  задает силу, точка приложения которой перемещается из начала в конец вектора
задает силу, точка приложения которой перемещается из начала в конец вектора  , то работа
, то работа  этой силы определяется равенством
этой силы определяется равенством

(20)
– физический смысл скалярного произведения.
ТЕОРЕМА 4. Модуль вектора (длина)  находится по формуле
находится по формуле
 .
.
(21)
ПРИМЕР 12. Вычислить работу равнодействующей  сил
сил
 ,
,  и
и 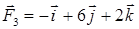 ,
,
приложенных к материальной точке, которая под их действием перемещается прямолинейно из точки  в точку
в точку  .
.
РЕШЕНИЕ. Так как равнодействующая сил  ,
,  , то работа
, то работа  вычисляется по формуле (13):
вычисляется по формуле (13):
 (дж).
(дж).
ПРИМЕР 13. Найти длину вектора 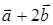 , если
, если  и
и 
РЕШЕНИЕ. Обозначим 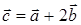 ,
,  , т. к.
, т. к.  . По формуле (14)
. По формуле (14) 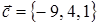 .
.
 .
.
ПРИМЕР 14. Найти длину вектора  , если известно
, если известно  ,
,  и
и  .
.
РЕШЕНИЕ. Обозначим  . Тогда длина вектора
. Тогда длина вектора

 .
.
(Использованы формулы (15) и (21)).
ОПРЕДЕЛЕНИЕ 10. Векторным произведением вектора  на вектор
на вектор  называется третий вектор
называется третий вектор 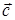 , определяемый следующим образом: (рис. 4)
, определяемый следующим образом: (рис. 4)
1. Модуль вектора 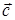 равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах  и
и  , то есть
, то есть
 ;
;
(22)
2. Вектор 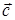 перпендикулярен векторам
перпендикулярен векторам  и
и  ;
;
3. Векторы  ,
,  ,
, 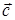 после приведения в общему началу образуют правую тройку векторов, то есть ориентированы по отношению друг к другу как базис
после приведения в общему началу образуют правую тройку векторов, то есть ориентированы по отношению друг к другу как базис 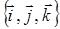 .
.















 |


Рис. 4
ТЕОРЕМА 5. Векторное произведение векторов  и
и  , заданных своими координатами, находится по формуле
, заданных своими координатами, находится по формуле
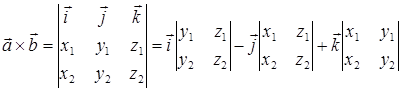 .
.
(23)
ПРИМЕР 15. Даны вершины треугольника  ,
,  и
и 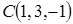 . Найти косинус угла
. Найти косинус угла  и площадь треугольника
и площадь треугольника  .
.
РЕШЕНИЕ. Угол  образован векторами
образован векторами  и
и  . Найдем координаты этих векторов по формуле (13):
. Найдем координаты этих векторов по формуле (13):
 ,
,  .
.
По формуле (17)
 .
.
Треугольник  является половиной параллелограмма, построенного на векторах
является половиной параллелограмма, построенного на векторах  и
и  . Тогда
. Тогда
 .
.
Найдем векторное произведение векторов по формуле (23):
 ;
;
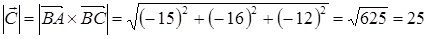 .
.
 (кв. ед.).
(кв. ед.).
Векторное произведение применяется в геометрии и механике для нахождения площади треугольника и параллелограмма (см. пример 15) и момента силы. Если вектор  задает силу, приложенную к какой-нибудь точке
задает силу, приложенную к какой-нибудь точке  , а вектор
, а вектор  идет из недвижимой точки
идет из недвижимой точки  в точку
в точку  , то вектор
, то вектор  представляет собой момент силы
представляет собой момент силы  относительно точки
относительно точки  – физический смысл векторного произведения.
– физический смысл векторного произведения.
ОПРЕДЕЛЕНИЕ 11. Если два вектора  и
и  умножить векторно
умножить векторно  , а полученный результат умножить на вектор
, а полученный результат умножить на вектор 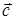 скалярно, то число
скалярно, то число 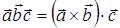 называется смешанным произведением трех векторов
называется смешанным произведением трех векторов  ,
,  ,
, 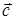 .
.
ТЕОРЕМА 6. Смешанное произведение трех векторов  ,
,  и
и 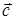
 находится с помощью определителя третьего порядка:
находится с помощью определителя третьего порядка:
 .
.
(24)
Необходимым и достаточным условием компланарности трех векторов служит условие
 .
.
(25)
ТЕОРЕМА 7. Смешанное произведение трех векторов  ,
,  ,
, 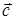 по модулю равно объему параллелепипеда, построенного на этих векторах, как на сторонах:
по модулю равно объему параллелепипеда, построенного на этих векторах, как на сторонах:
 .
.
(26)
ПРИМЕР 16. Найти объем треугольной призмы, построенной на векторах  ,
,  ,
,  .
.
РЕШЕНИЕ. Объем призмы равен половине объема параллелепипеда, построенного на векторах  ,
,  и
и 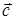 . Тогда по формуле (26) имеем
. Тогда по формуле (26) имеем
 .
.
Запишем координаты векторов  ,
,  и
и 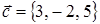 .
.
Найдем смешанное произведение по формуле (24):

 .
.
Тогда  (куб. ед.).
(куб. ед.).
12. ПРЯМАЯ НА ПЛОСКОСТИ
ТЕОРЕМА 8. В декартовой прямоугольной системе координат  на плоскости любая прямая может быть задана уравнением первой степени относительно
на плоскости любая прямая может быть задана уравнением первой степени относительно 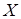 и
и  :
:

(27)
где  ,
,  и
и  – коэффициенты (при условии
– коэффициенты (при условии 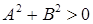 , то есть хотя бы одно из чисел
, то есть хотя бы одно из чисел  и
и  не равно нулю), и обратно, всякое уравнение вида (27) определяет прямую.
не равно нулю), и обратно, всякое уравнение вида (27) определяет прямую.
Если  , то уравнение примет вид
, то уравнение примет вид  или
или  – это уравнение прямой, параллельной оси
– это уравнение прямой, параллельной оси 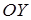 .
.
Аналогично 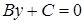 – уравнение прямой, параллельной оси
– уравнение прямой, параллельной оси  .
.
Уравнение (27) называется общим уравнением прямой.
Если  , то уравнение
, то уравнение  можно разрешить относительно
можно разрешить относительно  и представить в виде
и представить в виде
 , где
, где 
(28)
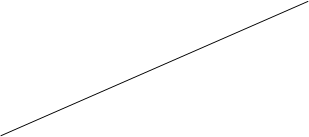
Последнее уравнение называется уравнением прямой с угловым коэффициентом  . Угол
. Угол 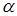 , отсчитываемый от положительного направления оси
, отсчитываемый от положительного направления оси  до прямой, называется углом наклона прямой, а число
до прямой, называется углом наклона прямой, а число 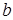 определяет начальную ординату, то есть величину отрезка, отсекаемого прямой на оси
определяет начальную ординату, то есть величину отрезка, отсекаемого прямой на оси 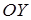 (рис. 5).
(рис. 5).



|


0 
Рис. 5
Если прямые заданы уравнениями 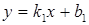 и
и  , то угол
, то угол  между ними находится по формуле
между ними находится по формуле

(29)
Условием параллельности двух прямых является равенство их угловых коэффициентов 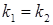 , а для их перпендикулярности необходимо и достаточно, чтобы
, а для их перпендикулярности необходимо и достаточно, чтобы  , то есть
, то есть  .
.
(30)
ПРИМЕР 17. Вычислить величину меньшего угла  между прямыми
между прямыми  и
и  .
.
РЕШЕНИЕ. Разрешим общие уравнения прямых относительно переменной  :
:  и
и 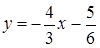 .
.
Отсюда следует, что угловые коэффициенты прямых  ,
,  , так как
, так как  , то прямые пересекаются, и по формуле (29)
, то прямые пересекаются, и по формуле (29)

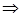
 .
.
Острый угол  =
= 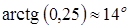
 .
.
Существуют и другие виды уравнений прямой на плоскости:
1) Уравнение прямой в «отрезках»:
 ,
,
(31)
где  – отрезок, отсекаемый на оси
– отрезок, отсекаемый на оси  ,
, 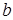 – на оси
– на оси 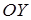 .
.
2) Уравнение через точку  и угловой коэффициент
и угловой коэффициент  :
:
 .
.
(32)
ПРИМЕР 18. Через точки  и
и  проведена прямая
проведена прямая  . Проходит ли она через начало координат?
. Проходит ли она через начало координат?
РЕШЕНИЕ. Возьмем на данной прямой еще одну текущую точку  . Пусть координаты этой точки
. Пусть координаты этой точки  . Тогда векторы
. Тогда векторы  и
и 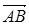 лежат на одной прямой, то есть они коллинеарны. Найдем координаты векторов
лежат на одной прямой, то есть они коллинеарны. Найдем координаты векторов  и
и 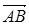 :
:  и
и  . Из условий коллинеарности двух векторов (формула 14) получаем уравнение прямой
. Из условий коллинеарности двух векторов (формула 14) получаем уравнение прямой  :
:
 .
.
Отсюда 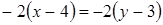 или
или  .
.
Прямая не проходит через начало координат, так как точка 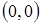 не удовлетворяет уравнению прямой:
не удовлетворяет уравнению прямой: 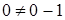 .
.
ПРИМЕР 19. Точка  лежит на прямой, перпендикулярной к прямой
лежит на прямой, перпендикулярной к прямой  . Найти уравнение этой прямой.
. Найти уравнение этой прямой.
РЕШЕНИЕ. Определим угловой коэффициент первой прямой:  , отсюда
, отсюда  . С учетом перпендикулярности прямых (формула 30)
. С учетом перпендикулярности прямых (формула 30)  . Тогда уравнение второй прямой можно найти по формуле (32):
. Тогда уравнение второй прямой можно найти по формуле (32):
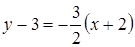 или
или 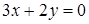 .
.
13. ПЛОСКОСТЬ
ТЕОРЕМА 9. В декартовых прямоугольных координатах уравнение любой плоскости приводится к виду
 ,
,
(33)
где  ,
,  ,
,  и
и  – заданные числа, причем
– заданные числа, причем  , и обратно, уравнение (33) всегда является уравнением плоскости.
, и обратно, уравнение (33) всегда является уравнением плоскости.
Уравнение (33) называется общим уравнением плоскости. Коэффициенты  ,
,  и
и  являются координатами нормального вектора
являются координатами нормального вектора  , то есть вектора, перпендикулярного к плоскости.
, то есть вектора, перпендикулярного к плоскости.
Существуют различные способы задания плоскости в  и соответствующие им виды уравнений.
и соответствующие им виды уравнений.
1. Уравнение плоскости, проходящей через точку 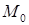 и перпендикулярной вектору
и перпендикулярной вектору  .
.
Если плоскость проходит через точку  и перпендикулярна вектору
и перпендикулярна вектору  , то ее уравнение записывается в виде
, то ее уравнение записывается в виде
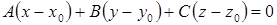
(34)
2. Уравнение плоскости, проходящей через три точки. Если плоскость проходит через три точки  ,
,  и
и  , не лежащие на одной прямой, то ее уравнение можно записать в виде
, не лежащие на одной прямой, то ее уравнение можно записать в виде

(35)
Раскрывая определитель по элементам первой строки, придем к общему уравнению плоскости (33).
3. Уравнение плоскости в «отрезках» (рис. 6).
 |
Дата добавления: 2015-10-26; просмотров: 170 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| A. Customs Inspection of the Baggage | | | Кубок «Газпром нефти» по решению нефтегазовых кейсов |