Активная среда

ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИK

ПОЛУПРОВОДНИКОВЫХ ИЗЛУЧАТЕЛЕЙ

Целью данной работы является теоретическое и экспериментальное исследование основных характеристик полупроводниковых лазеров (спектра излучения, поперечных и продольных мод, ватт-амперной характеристики, числовой апертуры), расчёты когерентности, изучение особенностей механизма генерации.

Введение

ЛАЗЕР (lightwave amplification by stimulated emission of radiation) - усиление световых волн с помощью стимулированного излучения.

Полупроводниковый лазер - это излучающий полупроводниковый прибор, предназначенный для непосредственного преобразования электрической энергии в энергию когерентного излучения.

Для возникновения лазерного излучения необходимо создать инверсную населённость. Инверсию в полупроводниковом р-n-переходе можно получить различными способами: инжекцией, пробоем в электрическом поле, электронной накачкой, оптической накачкой. Наиболее распространены полупроводниковые лазеры с инжекцией носителей зарядов, где увеличение концентрации носителей заряда в полупроводнике происходит в результате переноса их из областей с повышенной концентрацией под действием внешнего электрического поля.

К основным преимуществам полупроводниковых лазеров относятся: малые размеры; компактность; простота подключения; высокий КПД преобразования энергии накачки в энергию излучения; возможность питания от низковольтных источников; быстродействие (модуляции излучения лазера с частотой более 1 ГГц).

К недостаткам можно отнести бльшую по сравнению с газовыми лазерами расходимость пучка и малую временную когерентность.

Полупроводниковые лазеры используются в оптической связи, системах считывания, обработки и записи информации, медицине и др.

Принцип работы полупроводникового лазера

В основе принципа действия лазера лежат три физических явления: инверсия населённости, вынужденное излучение и положительная обратная связь.

Лазер состоит из трёх основных элементов: активной среды (активного элемента), в которой создается инверсия населённости; источника накачки; устройства, обеспечивающего положительную обратную связь (оптический резонатор).

Активная среда

В 1729 г. французский физик П. Бугер открыл закон ослабления параллельного пучка света в веществе:

S(x) = S(0) exp(- k x), (1.1)

где S(x) и S(0) - плотности светового потока в точках с координатами x и 0 соответственно; k - коэффициент поглощения света веществом, зависящий от длины волны света. Величина, обратная k, имеет физический смысл толщины слоя, в котором свет ослабляется в е раз.

Если кроме поглощения в веществе происходит рассеяние света, то

S(x) = S(0) exp{-(k + r)x}, (1.2)

где r - коэффициент рассеяния. Все без исключения тела в условиях термодинамического равновесия или незначительного отклонения от него поглощают и рассеивают излучение, при этом значение k + r изменяется от 10^-6 см^-1 в оптическом стекле до 10⁶ см^-1 в полупроводниках и металлах. Если в формуле (1.2) положить k + r < 0, то S(x) будет больше, чем S(0). Это означает, что свет, проходя через вещество с отрицательным показателем преломления, не ослабляется, а усиливается. Вещество, обладающее способностью усиливать электромагнитное излучение, называют активной средой.

В рамках квантовой теории процессы поглощения и испускания излучения веществом впервые были рассмотрены А. Эйнштейном в 1916 г. [1]. Он постулировал, что излучательные переходы с более высоких энергетических уровней на более низкие могут быть двух типов - спонта́нные и вынужденные. За единицу времени происходит A_ijn_i спонтанных переходов, а также B_iju⁰(n_ij)n_i и B_jiu⁰(n_ij)n_j вынужденных переходов с испусканием и поглощением квантов света (здесь A_ij ,B_ij,B_ji - коэффициенты Эйнштейна для спонтанных и вынужденных переходов; u⁰(n_ij) - спектральная плотность излучения на частоте n_ij; n_i, n_j - концентрации атомов с энергиями E_i и E_j соответственно). Энергия фотонов при этом равна

hn_ij = E_i – E_j,

где h - постоянная Планка.

В условиях термодинамического равновесия число поглощенных квантов равно числу испущенных:

A_ij n_i + B_ij u⁰(n_ij) n_i = B_ji u⁰(n_ij) n_j.

Поскольку A_ij и B_ij не зависят от u⁰(n_ij), то, полагая u⁰(n_ij)® ¥ и учитывая формулу Больцмана, описывающую распределение частиц по уровням

, (1.3)

находим

g_iB_ij = g_jB_ji,

где к – постоянная Больцмана; g_i и g_j- степени вырождения соответствующих уровней.

С учётом вынужденных переходов число квантов падающего излучения с плотностью энергии u⁰(n_ij), поглощённых в единице объёма в единицу времени, будет равно

N_n(n_ij) = B_jiu⁰(n_ij)n_j - B_iju⁰(n_ij)n_i = B_jiu⁰(n_ij)(n_j - g_jn_i/g_i). (1.4)

Здесь вынужденное излучение (второе слагаемое) фигурирует как отрицательное поглощение.

Если _, (1.5)

то согласно (1.4) поглощение в целом окажется отрицательным, т.е. будет происходить усиление излучения.

Это реализуется, когда на верхнем уровне в расчёте на одно квантово-механическое состояние частиц больше, чем на нижнем. Поскольку в условиях термодинамического равновесия населённость уровней экспоненциально убывает с ростом их энергии, то неравенство (1.5) является условием инверсной населённости.

В полупроводниках имеются широкие разрешённые и запрещённые зоны энергии, примесные уровни (примесные зоны).

В оптических явлениях невырожденных полупроводников наиболее важную роль играют квантовые переходы вблизи экстремальных точек зонной структуры. Эти области можно аппроксимировать моделью параболических зон (рис. 1.1):

Рис. 1.1. Модель параболических зон:

а - зоны энергии; б - зависимость энергии

электрона E от волнового вектора К

Уровни энергии в валентной зоне обозначим Е_v, в зоне проводимости - Е_c, ширину запрещённой зоны - Е_g, функции плотности состояний - соответственно g_v(E_v) и g_c(E_c).

Пусть реализуются только прямые оптические переходы, когда волновой вектор электрона сохраняется.

Обозначая коэффициент поглощения при межзонных переходах и отсутствии возбуждения 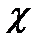(n), для возбуждённой системы можно получить

k (n) = (n)[f_n(E_v) – f_p(E_c)]. (1.6)

Здесь

;

(1.7)

есть функции Ферми-Дирака, описывающие распределение электронов в валентной зоне и зоне проводимости E_c - E_v = = hn; F_n и F_p - квазиуровни Ферми для электронов и дырок соответственно.

Если общее число электронов в зоне проводимости равно n, а дырок в валентной зоне p, то значения квазиуровней Ферми определяются из условий

,

,

где E_co и E_vo - энергии дна зоны проводимости и потолка валентной зоны соответственно (рис. 1.1). Согласно (1.6) c(n) равно значению коэффициента поглощения при условии, что все состояния в валентной зоне заняты, а в зоне проводимости свободны, т.е. f_n(E_v) = 1, f_n(E_c) = 0.

В (1.6) предполагается, что, хотя в целом квантово-механическая система выведена из состояния термодинамического равновесия, в отдельных зонах устанавливается равновесное распределение электронов, описываемое функциями (1.7). Уравнение (1.6) выполняется в широких пределах, в том числе и при возбуждении полупроводников сверхкороткими лазерными импульсами, поскольку времена релаксации в зонах равны 10^-11... 10^-12 с.

Из условия k(n) < 0 с помощью (1.6) и (1.7) и при eU = F_n – F_p находим условие инверсной населённости для полупроводниковых лазеров:

e U = F_n – F_p > E _g» hn. (1.8)

Итак, для создания инверсной населённости необходимо приложить к p-n-переходу такое напряжение, чтобы разность уровней Ферми для электронов и дырок была больше ширины запрещённой зоны.

Дата добавления: 2015-10-26