
Читайте также:
|
Как мы уже знаем, эластичность позволяет нам оценить реакцию какого-либо результата на изменение какого-либо фактора.
По способам расчета коэффициента эластичности спроса выделяют точечную и дуговую эластичность.
Для того чтобы увидеть различия в этих способах, еще раз вернемся к формуле эластичности (8.3):
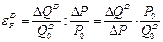
при этом в качестве Q0D и P0 возьмем начальные значения цены и объема спроса.
| ПРИМЕР | Рассмотрим следующий пример:
Пусть цена блага выросла с 10 до 20 рублей за единицу, тогда объем спроса снизился со 50 до 40 единиц.
Начальными значениями (в точке А) являются цена в 10 рублей за единицу, а объем спроса — 50 единиц, а эластичность спроса равна:
Однако, очевидно, что при изменении цены в противоположном направлении (при переходе из точки B в точку A), объем спроса также должен измениться в противоположном направлении, при этом абсолютные изменения будут такими же. То есть, если цена блага снизилась с 20 до 10 рублей за единицу, объем спроса вырастет с 40 до 50 единиц. |
| ПРИМЕР (продолжение) | Предположим теперь, что (поскольку абсолютные изменения цены и объема спроса при переходе из точки B в точку A остались теми же, что при переходе из точки A в точку B – изменилось лишь направление движения по кривой спроса), эластичность спроса также не должна измениться (то есть относительные изменения также будет одинаковыми).
При перемещении из точки B в точку A (при повышении цены блага), начальные значения цены и объема спроса составляют 20 рублей и 40 единиц. Рассчитаем новый коэффициент ценовой эластичности спроса, учитывая в качестве начальных значения в точке B (P1 и Q1D):
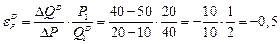 .
Как видим, наше предположение оказалось неверным: одинаковые изменения цены и объема спроса при разных направлениях этих изменений привели к разным значениям ценовой эластичности. .
Как видим, наше предположение оказалось неверным: одинаковые изменения цены и объема спроса при разных направлениях этих изменений привели к разным значениям ценовой эластичности.
|
Почему же так произошло? Дело в том, что при расчете относительных изменений любой величины мы обязаны учитывать исходные значения этой величины. В точке A меньше, а объем спроса больше, нежели в точке B. Следовательно, одинаковым абсолютным изменениям этих параметров соответствуют разные относительные.
Использованный нами способ расчета эластичности спроса, называется точечной эластичностью (point elasticity) или эластичностью спроса по цене в окрестностях точки A.
| ! | Обратите внимание! Точечная эластичность показывает, насколько эластичен спрос в данной точке. Ее имеет смысл использовать в тех случаях, когда изменение аргумента является незначительным (обычно незначительным мы считаем изменение параметра менее чем на 10%, хотя показатель точечной эластичности будет наилучшим образом характеризовать чувствительность изменения функции при изменении значения аргумента при условии, что изменение аргумента будет стремиться к 0). |
Что же делать в ситуации, когда нам необходимо оценить эластичность при больших изменениях значений аргумента и самой функции? Для этого существует иной способ расчета эластичности. Как мы помним, эластичность интересует нас в качестве показателя, характеризующего изменения. То есть нас интересует поведение величины спроса на всем участке AB.
Точечная эластичность, посчитанная в точке A, неплохо характеризует изменения вблизи точки А, но мало подходит для анализа изменений «в районе» точки B. Наоборот, точечная эластичность, рассчитанная в точке B, не показательна для оценки поведения функции около точки A. Как же посчитать эластичность в этом случае? То есть, какую точку выбрать за «точку отсчета», относительно которой мы будем оценивать изменения? Логично предположить, что это может быть некая точка C1, которая находится в середине дуги AB, то есть AC1 = BC1.
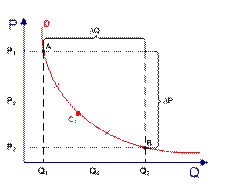
Проблемой является то, что наша функция задана дискретно, то есть кроме координат точек A и B мы не знаем о ней ничего. Поэтому определить координаты точки C1 невозможно.
Как же поступить в данном случае? Проведя отрезок (хорду) AB, можно найти координаты ее середины – точки C. Точка C и будет той единственной точкой, которая находится относительно близко к точке C1, координаты которой мы можем определить.
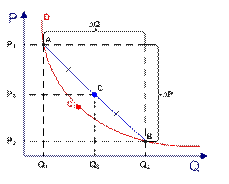
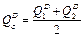
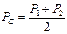
Тогда эластичность спроса по цене на участке AB можно посчитать, учитывая координаты точки C:
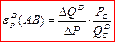 (8.4)
(8.4)
Такой вид эластичности (рассчитанной с использованием координат середины отрезка AB) называется дуговой эластичностью (arc elasticity).
Дуговая эластичность используется при значительных (более 10%) изменениях аргумента и значения функции)
Таким образом, для расчета дуговой эластичности спроса по цене мы можем использовать следующую формулу:
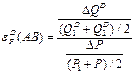
Преобразовав ее, получим:
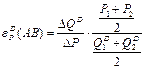
Сократив «двойки» в числителе и знаменателе, получим формулы, представленные в более удобном виде:
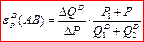 или или 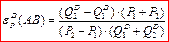 ,
которые аналогичны формуле 8.4 ,
которые аналогичны формуле 8.4
| (8.5) |
Очевидно, что использование дуговой эластичности позволяет определить только приблизительное значение эластичности на дуге AB. Погрешность вычислений будет определяться изгибом дуги AB, и будет тем больше, чем более вогнутой к началу координат окажется дуга AB.
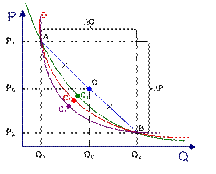
| ПРИМЕР (продолжение) | В нашем примере, когда цена блага выросла с 10 до 20 рублей за единицу и объем спроса снизился со 50 до 40 единиц.
Для того чтобы получить результат, не зависящий от направления изменения цены и объема спроса, используем координаты точки C – середины отрезка AB:
Тогда
или (сократив «двойки»)
|
| ! | Обратите внимание! Дуговая эластичность показывает, насколько эластичен спрос на участке функции. Анализ дуговой эластичности имеет смысл использовать в тех случаях, когда изменение аргумента является достаточно большим (обычно более 10%). |
При относительно больших (более 10%) изменениях цены (и объема спроса) используется дуговая эластичностьспроса по цене.
| ЗАДАЧА 4 | Решение задачи. Определение дуговой эластичности спроса на книги по цене. Издательство обнаружило, что по цене 60 руб. оно может реализовать 1000 экз. книг в неделю, а по цене 80 руб. - 900 экз. Определите дуговую эластичность спроса на книги по цене. Пожалуйста, подтвердите ответ вычислениями. |
При анализе функции спроса, представленной в табличном или графическом виде, данный способ является более предпочтительным.
Дата добавления: 2015-10-24; просмотров: 380 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ценовая эластичность спроса | | | Вычисление ТОЧЕЧНОЙ эластичности через отношение отрезков (в точке C) |