Приклад розв’язування задачі Д4

Умова задачі. Точка D масою m = 0,5кг починає рухатись по трубці АВ з початковою швидкістю V_o= 10м/с, де на неї крім сили ваги діє постійна сила F = 10Н і сила опору пропорційна квадрату швидкості R=0,8 V^{2 .}. Точка D проходить шлях АВ = l = 1м і в точці В потрапляє на ділянку ВС, де на неї крім ваги діє сила тертя з коефіцієнтом тертя f = 0,1 і змінна сила H = 40sin(pt). Положення ділянок АВ і ВС та напрямки сил F і H показано на рис. Д4.6.

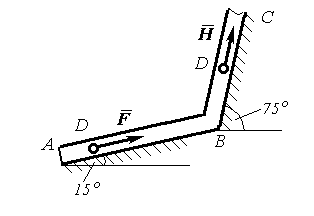
Рис. Д4.6

Знайти шлях як функцію від часу для точки D на ділянці ВС x(t) та залежність швидкості від часу V(t) на цій же ділянці. Побудувати графіки цих залежностей.

Розв’язання. Складаємо диференціальне рівняння руху точки D на ділянці АВ. Зображаємо сили, що діють на точку D на цій ділянці, і показуємо їх на рис. Д4.7.

Рис. Д4.7

Застосовуємо диференціальне рівняння руху точки, яке в проекції на вісь х має вигляд

. (4.1)
Знаходимо суму проекцій сил на вісь x

.

Тому отримуємо

. (4.2)

Переходимо в диференціальному рівнянні (4.2) від змінної t до змін-ної x. Цей перехід обумовлений тим, що в умові задачі дано, що ру-хома точка D досягає певної швидкості в точці В після того, як вона пройшла шлях АВ.

. (4.3)

Розділимо змінні і запишемо інтеграл
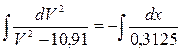, звідки отримуємо
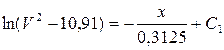. (4.4)

Початковою умовою для цього інтеграла буде при x = 0,
тому .

Тоді інтеграл (4.3) має остаточний вигляд

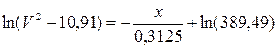. (4.5)

При умові, що х=АВ = l = 1м маємо, що V = V_B. З виразу (4.5) знаходимо

м/с. (4.6)

Складаємо диференціальне рівняння руху точки D на ділянці ВС. Вказуємо сили, які діють на точку і показуємо їх на рисунку Д4.8.

Знаходимо суму проекцій сил на вісь Bx.

,

де .

Підставляємо її в рівняння (4.1)

.

Рис.Д4.8

Після підстановки даних умови одержуємо диференціальне рівняння руху точки D на ділянці ВС.

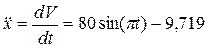. (4.7)

Звідки записуємо інтеграл

.

Після інтегрування одержуємо

.

Початковою умовою для цього інтеграла буде при t = 0,
тому стала інтегрування С₃ рівна

.

Остаточно перший інтеграл диференціального рівняння (4.7) буде

. (4.8)

Знаходимо залежність координати x від часу. Оскільки , тому

.

Після інтегрування одержуємо

.

Початковою умовою для цього інтеграла буде x = 0 при t = 0, тому

С₄ =0. Остаточно залежність x(t) має вигляд:

. (4.9)

Числові значення залежності шляху від часу x(t) і швидкості від часу V(t) одержуються за формулами (4.9) і (4.8). Графіки вказаних функцій побудовані в програмі EXEL наведені на рисунках Д4.9 і Д4.10.

Рис. Д4.9

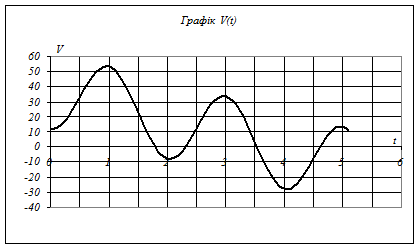Рис. Д4.10

Дата добавления: 2015-09-04