Пример 3. Рассмотрим переходный процесс в линейной электрической цепи второго порядка

Рассмотрим переходный процесс в линейной электрической цепи второго порядка, вызванный подключение ветви, содержащей сопротивление 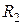и емкость (рис. 4.8), выбрав в качестве реакции ток 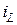, протекающий через индуктивность.

Рис. 4.8

Поскольку цепь содержит два узла и три ветви, то для описания протекающих в ней процессов необходимо записать одно уравнение по первому закону Кирхгофа и два – по второму. Однако один из токов ветвей является задающим током источника и считается известным. Следовательно, по второму закону Кирхгофа будет составлено лишь одно уравнение. Дополним систему компонентными соотношениями. Получим:

(4.31)

Сведем систему (4.31) к дифференциальному уравнению для тока 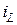. С этой целью подставим выражения для 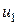, и 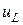во второе уравнение системы. Получим:

(4.32)

Выразим ток из первого уравнения и подставим во второе и третье:

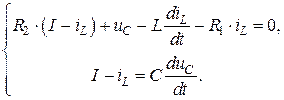(4.33)

Выразим из первого уравнения и подставим во второе. После приведения подобных и деления всего уравнения почленно на получим:

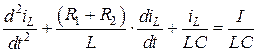. (4.34)

Введем обозначения:

Пусть 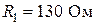, , , , . Тогда:

Поскольку , то характер переходного процесса – колебательный. Значит свободная составляющая тока, протекающего через индуктивность равна:

, (4.35)

Вынужденную составляющую тока, протекающего через индуктивность , найдем, исключив обе производные из дифференциального уравнения (4.34):

. (4.36)

Тогда общее решение уравнения (4.34) имеет вид:

. (4.37)

Для определения констант интегрирования и 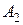найдем зависимые и независимые начальные условия. Рассмотрим цепь в момент времени , предшествующий замыканию ключа (рис. 4.9).

Рис. 4.9

Поскольку цепь одноконтурная, то элементы соединены последовательно и во всей цепи протекает один и тот же ток, равный задающему току источника:

.

Поскольку до замыкания ключа емкость была отключена, то напряжение на ней:

.

Тогда согласно законам коммутации:

, .

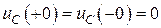Рассмотрим цепь в момент времени , следующий сразу за замыканием ключа, и определим зависимое начальное условие (рис. 4.10).

Рис. 4.10

Поскольку в цепи действует два источника, то суммарное напряжение найдем как сумму напряжений и , отражающих реакцию цепи на действие каждого из источников в отдельности (метод наложения). Поочередное гашение источников тока приводит к цепям, изображенным на рис. 4.11.

Рис. 4.11

Для цепи на рис. 4.11, а токи и 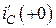имеют одинаковое абсолютное значение, равное задающему току источника, но противоположны по направлению. Значит, второй закон Кирхгофа для этой одноконтурной цепи имеет вид:

Для цепи на рис. 4.11, б ток 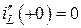, а ток согласно первому закону Кирхгофа равен задающему току источника . Тогда уравнение, составленное по второму закону Кирхгофа для выбранного контура, имеет вид:

.

Тогда зависимое начальное условие для напряжения на емкости:

.

Запишем общее выражение для напряжения 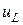, воспользовавшись (4.37) и компонентным соотношением для индуктивности:

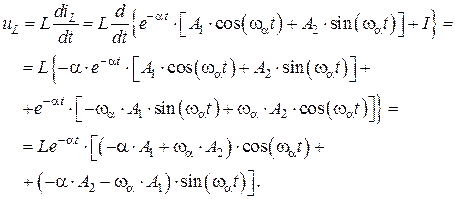(4.38)

Подстановка найденных начальных условий в (4.37) и (4.38) дает следующую систему уравнений для нахождения и :

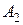(4.39)

Из первого уравнения системы (4.39) находим, что 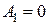. Тогда из второго уравнения следует, что . Тогда ток, протекающий через индуктивность, имеет вид:

. (4.40)

На рис. 4.12 представлен график изменения тока со временем.

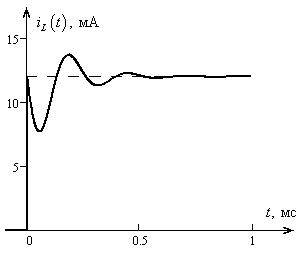
Рис. 4.12

Дата добавления: 2015-09-04