
Читайте также:
|
Краткие теоретические сведения
Основы символического метода анализа цепей
Гармоническими токами и напряжениями называют токи и напряжения, мгновенное значение которых изменяется во времени по гармоническому закону.
Гармонические колебания являются простейшим видом периодических колебаний, которые удовлетворяют условию
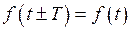 , (1.1)
, (1.1)
где  - функция, определяющая зависимость мгновенного значения тока или напряжения от времени;
- функция, определяющая зависимость мгновенного значения тока или напряжения от времени;  - период колебания.
- период колебания.
Величину  называют циклической (линейной) частотой. Циклическая частота равна числу полных колебаний в единицу времени и измеряется в герцах (Гц), килогерцах (кГц), мегагерцах (МГц) и т.д.
называют циклической (линейной) частотой. Циклическая частота равна числу полных колебаний в единицу времени и измеряется в герцах (Гц), килогерцах (кГц), мегагерцах (МГц) и т.д.
Периодом  колебания называют наименьший интервал времени, по истечении которого значения колеблющейся величины повторяются. Период колебания измеряется в единицах времени: секундах (с), миллисекундах (мс), микросекундах (мкс) и т.д.
колебания называют наименьший интервал времени, по истечении которого значения колеблющейся величины повторяются. Период колебания измеряется в единицах времени: секундах (с), миллисекундах (мс), микросекундах (мкс) и т.д.
Все пояснения сопровождаются иллюстрациями и записями зависимостей на примере колебаний напряжения 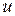 . Однако рассматриваемые положения в такой же мере относятся и к колебаниям тока.
. Однако рассматриваемые положения в такой же мере относятся и к колебаниям тока.
Гармонические колебания токов и напряжений следует записывать в виде
 , (1.2)
, (1.2)
или сводить к такой зависимости. График этого гармонического колебания напряжения приведен на рис.1.1.

Рис. 1.1. Графики гармонических колебаний.
Строго говоря, гармоническое колебание существует на всей оси времени, то есть от  до
до  . Оно бесконечно давно началось и никогда не окончится, чего в реальности, естественно, нет. Однако иногда для упрощения рассуждений гармоническими колебаниями называют и колебания, подчиняющиеся закону косинуса на конечных интервалах времени.
. Оно бесконечно давно началось и никогда не окончится, чего в реальности, естественно, нет. Однако иногда для упрощения рассуждений гармоническими колебаниями называют и колебания, подчиняющиеся закону косинуса на конечных интервалах времени.
Максимальное значение по модулю, которое принимает колеблющаяся величина, называется её амплитудным значением, или амплитудой. В теории электрических цепей говорят об амплитуде напряжения  , об амплитуде э.д.с.
, об амплитуде э.д.с.  , об амплитуде тока
, об амплитуде тока  . Амплитуда - величина сугубо положительная.
. Амплитуда - величина сугубо положительная.
Величину  , измеряемую в радианах, называют мгновенной фазой, или фазой колебания. Фаза характеризует стадию колебания в рассматриваемый момент времени. Скорость изменения мгновенной фазы
, измеряемую в радианах, называют мгновенной фазой, или фазой колебания. Фаза характеризует стадию колебания в рассматриваемый момент времени. Скорость изменения мгновенной фазы  называется угловой частой. Угловая частота измеряется в радианах в секунду (рад/с). После увеличения мгновенной фазы на 2π радиан весь цикл колебаний повторяется. Угловая частота связана с периодом
называется угловой частой. Угловая частота измеряется в радианах в секунду (рад/с). После увеличения мгновенной фазы на 2π радиан весь цикл колебаний повторяется. Угловая частота связана с периодом  колебания и циклической частотой
колебания и циклической частотой  простой зависимостью
простой зависимостью
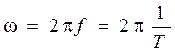 . (1.3)
. (1.3)
Несложно понять, что угловая частота является производной по времени от мгновенной фазы
 . (1.4)
. (1.4)
Значение 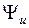 мгновенной фазы в момент начала отсчета времени
мгновенной фазы в момент начала отсчета времени  называют начальной фазой. При записи гармонического колебания косинусоидальной функцией значение
называют начальной фазой. При записи гармонического колебания косинусоидальной функцией значение 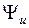 на графике отсчитывается от точки
на графике отсчитывается от точки  до ближайшего максимума. Если ближайший максимум расположен слева от нулевой точки, то
до ближайшего максимума. Если ближайший максимум расположен слева от нулевой точки, то 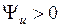 (рис.1.1а), в противном случае
(рис.1.1а), в противном случае 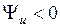 (рис.1.1. в). Колебание, сдвинутое вправо по оси времени, является запаздывающим по сравнению с колебанием, не имеющим такого сдвига.
(рис.1.1. в). Колебание, сдвинутое вправо по оси времени, является запаздывающим по сравнению с колебанием, не имеющим такого сдвига.
В электрической цепи находящейся под воздействием источников гармонических токов и напряжений, по истечении достаточно большого промежутка времени устанавливаются колебания напряжении и токов, которые можно считать гармоническими. Такой режим электрической цепи называют режимом установившихся гармонических колебаний (установившимся режимом).
На практике для нахождения гармонических токов и напряжений в цепи широкое применение получил векторный метод анализа цепей и метод комплексных амплитуд.
Векторный метод основан на представлении гармонических токов и напряжении вращающимися векторами. Вращающийся вектор в свою очередь может быть выражен комплексной функцией. Эту функцию называют комплексным мгновенным значением гармонического колебания и записывают так:
 . (1.5)
. (1.5)
При этом само гармоническое колебание и называют функцией-оригиналом, а комплексное мгновенно значение  - функцией-изображением, или символическим изображением функции-оригинала. Связь между функцией-оригиналом и функцией изображением однозначная. Она определяется с помощью формулы Эйлера
- функцией-изображением, или символическим изображением функции-оригинала. Связь между функцией-оригиналом и функцией изображением однозначная. Она определяется с помощью формулы Эйлера
 . (1.6)
. (1.6)
Вещественная часть этого выражения есть не что иное, как функция-оригинал, или мгновенное значение гармонического колебания. Таким образом, чтобы найти гармоническое колебание по известному его комплексному мгновенному значению, необходимо записать его в алгебраической форме и взять его вещественную часть. Эта операция символически может быть записана так:
 . (1.7)
. (1.7)
Символ Re означает операцию взятия вещественной части от комплексной величины.
Комплексное мгновенное значение может быть записано иначе
 (1.8)
(1.8)
При этом сомножитель 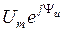 , определяющий положение вращающегося вектора
, определяющий положение вращающегося вектора 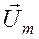 на комплексной плоскости в момент
на комплексной плоскости в момент  называют комплексной амплитудой и обозначают
называют комплексной амплитудой и обозначают  . Таким образом, комплексная амплитуда
. Таким образом, комплексная амплитуда
 .
.
Модуль комплексной амплитуды 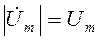 равен амплитуде гармонического колебания, а аргумент комплексной амплитуды равен начальной фазе гармонического колебания:
равен амплитуде гармонического колебания, а аргумент комплексной амплитуды равен начальной фазе гармонического колебания:
 .
.
Используя понятие комплексной амплитуды, соотношение (1.7) можно записать в виде:
 . (1.9)
. (1.9)
Поскольку векторные диаграммы обычно изображаются для момента  , то векторы на комплексной плоскости, изображающие гармонические колебания токов, напряжений и ЭДС, соответственно обозначают
, то векторы на комплексной плоскости, изображающие гармонические колебания токов, напряжений и ЭДС, соответственно обозначают
 .
.
При известной угловой частоте  комплексную амплитуду можно рассматривать как изображение гармонического колебания, т.е.:
комплексную амплитуду можно рассматривать как изображение гармонического колебания, т.е.:
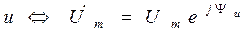 (1.10)
(1.10)
аналогично
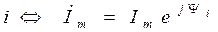
 . (1.11)
. (1.11)
Вместо комплексной амплитуды можно рассматривать комплексную величину, модуль которой в  раз меньше комплексной амплитуды. Эту комплексную величину называют комплексным действующим значением и обозначают
раз меньше комплексной амплитуды. Эту комплексную величину называют комплексным действующим значением и обозначают  . Таким образом:
. Таким образом:
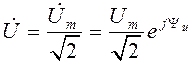 . (1.12)
. (1.12)
Комплексное действующее значение иногда называют просто комплексом напряжения, тока или ЭДС. Поскольку комплексное действующее значение пропорционально комплексной амплитуде, все, что говорится о комплексной амплитуде, относится и к комплексному действующему значению. Сложение гармонических колебаний можно заменить сложением их векторов, или комплексных амплитуд.
Преимущество символического метода состоит в простоте вычислений и возможности получить достаточно обобщенные выводы. Дополнение результатов анализа векторными диаграммами на комплексной плоскости делает этот метод наглядным.
Для комплексных амплитуд (комплексов) могут быть введены законы Кирхгофа, например:
 ,
,  (1.13)
(1.13)
это первый закон Кирхгофа в символической форме. Он формулируется так: алгебраическая сумма комплексных амплитуд (комплексов) токов в любом узле геометрической цепи равен нулю.
Алгебраичность суммы состоит в том, что знак каждого слагаемого определяется в соответствии с принятым направлением отсчета токов в каждой ветви, аналогично тому, как это делалось при записи уравнении для мгновенных значений тока.
Аналогично можно ввести выражение второго закона Кирхгофа в символической форме:
 . (1.14)
. (1.14)
Второй закон Кирхгофа в символической форме формулируется так: алгебраическая сумма комплексных амплитуд напряжений в любом контуре электрической цепи равна нулю.
Введение законов Кирхгофа для комплексных амплитуд (комплексов) позволяет составлять для них уравнения электрического равновесия, которые, в отличие от уравнений электрического равновесия для мгновенных значений, являются алгебраическими, а не интегро-дифференциальными. Эта система уравнений описывает гармонические колебания в цепи и может быть решена обычными алгебраическими методами.
Отношение комплексной амплитуды напряжения на зажимах двухполюсника, не содержащего независимых источников, к комплексной амплитуде тока, протекающего через эти зажимы, называют комплексным сопротивлением:
 ,
,  . (1.15)
. (1.15)
Эта запись формально аналогичная закону Ома получила название закона Ома в символической форме, или закона Ома для комплексных амплитуд. Величина, обратная комплексному сопротивлению, называется комплексной проводимостью и обозначается буквой Y.
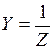 . (1.16)
. (1.16)
Используя понятие комплексной проводимости, можно привести еще одну запись закона Ома в символической форме
 . (1.17)
. (1.17)
Введение закона Ома для комплексных амплитуд (комплексов) наряду с законами Кирхгофа позволяет упростить составление уравнений электрического равновесия для комплексных амплитуд.
Порядок анализа цепи символическим методом рассмотрим на двух следующих примерах.
ПРИМЕР 1
Найти токи и напряжения ветвей приведенной на рис.1.2 цепи.
 РЕШЕНИЕ
РЕШЕНИЕ
Пусть  , что предполагает размещение вектора ЭДС источника вдоль оси вещественных чисел.
, что предполагает размещение вектора ЭДС источника вдоль оси вещественных чисел.
Анализируемую цепь можно рассматривать в качестве двухполюсника, состоящего из последовательно соединенных сопротивления и индуктивности, к которому присоединен источник ЭДС.
Находим комплексное входное сопротивление этого двухполюсника:
 .
.
По закону Ома находим ток в цепи и напряжения на ее ветках:
 ,
,
где  - аргумент комплексного входного сопротивления.
- аргумент комплексного входного сопротивления.
 ,
,
 .
.
Результат решения иллюстрируем векторной диаграммой рис.1.2. Здесь следует заметить, что треугольник, построенный из векторов напряжений, является замкнутым. Это положение является проявлением второго закона Кирхгофа в векторной форме для контура, который образует заданная цепь. Однако реальный анализ цепи ведется всегда с конечной точностью, и многоугольник векторов напряжений, построенный по результатам расчетов или измерений, далеко не всегда получается замкнутым. При этом точность анализа можно оценить по длине вектора, замыкающего многоугольник векторов напряжений. Аналогичное заключение можно сделать и относительно векторов токов относительно какого-либо узла цепи.
ПРИМЕР 2
Найти токи и напряжения ветвей приведенной на рис.1.3.а цепи.

РЕШЕНИЕ
Пусть  . Далее поступаем так же как в предыдущем примере.
. Далее поступаем так же как в предыдущем примере.
Находим комплексное входное сопротивление:
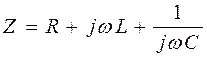 , или же
, или же
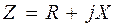 ,
,
где  – реактивная составляющая комплексного входного сопротивления.
– реактивная составляющая комплексного входного сопротивления.
По закону Ома находим ток в цепи и напряжение на её ветвях:
 ,
,
где  - аргумент комплексного входного сопротивления.
- аргумент комплексного входного сопротивления.
 ,
,
 ,
,
 .
.
Результат решения иллюстрируем векторной диаграммой рис.1.3, б. Здесь для иллюстрации выбран случай, которому соответствует  . Другими словами индуктивное сопротивление
. Другими словами индуктивное сопротивление  больше емкостного
больше емкостного 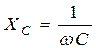 .
.
Дата добавления: 2015-09-04; просмотров: 81 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Бретелька, о которой узнал весь Нью Йорк | | | Описание лабораторной установки |