Ускорение точки при векторном способе задания движения.

По определению ускорение является производной по времени от вектора скорости:

(1)

Когда Δ 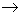0, точка M₁ 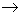M; плоскость, где лежат векторы (t), (t + Δt) и (Δt), содержащая две касательные к траектории в точках M и M1 (рис. 62), стремится занять положение соприкасающейся плоскости в точке M; сам вектор направлен в сторону вогнутости траектории.

Таким образом, вектор ускорения a лежит в соприкасающейся плоскости и всегда направлен в сторону вогнутости траектории.

Очевидно, что a является ускорением в данное мгновение времени или мгновенным ускорением, а средним ускорением за промежуток времени Δt называется отношение ΔV / Δt. Соответственно, размерностью ускорения будет м / с² (метр за секунду в квадрате).

Дата добавления: 2015-09-04