Способы задания движения точки.

Для задания движения точки можно использовать несколько способов. Мы рассмотрим три основных: 1) векторный, 2) координатный, 3) естественный.

Векторный способ. Положение движущейся точки M относительно тела отсчета O можно определить радиус-вектором точки r, соединяющим тело отсчета и точку (рис. 57).

При движении точки M радиус-вектор r будет изменяться по модулю и направлению с течением времени t, то есть

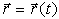
(1)

Выражение (1) определяет закон движения точки и является ее кинематическим уравнением движения в векторной форме.

Конец радиус-вектора совместно с точкой M движется в пространстве по кривой, которая является годографом радиус-вектора, а в кинематике называется траекторией точки. Движение точки по кривой называется криволинейным движением точки, если траектория точки - прямая линия, движение точки называется прямолинейным.

То обстоятельство, что радиус-вектор не связан с конкретной системой координат, позволяет широко использовать векторный способ задания движения для теоретических доказательств.

Для решения практических задач обычно используют координатный и естественный способы задания движения.

Координатный способ. Свяжем с телом отсчета систему координат Oxyz. Тогда положение точки M в системе отсчета можно определить тремя координатами точки x, y, z (рис. 57).

При движении точки M ее координаты будут изменяться с течением времени, то есть

x = x(t), y = y(t), z = z(t)

(2)

Выражения (2) определяют закон движения точки и являются ее кинематическими уравнениями в координатной форме.

Уравнения траектории точки можно получить из выражений (2), исключив из них время t. Например, из третьего уравнения в (2) выразим время: t = φ(z). Подставляя время в первые два уравнения, найдем уравнения траектории точки:

x = x(φ(z)), y = y(φ(z))

(3)

С телом отсчета может быть связана не только прямоугольная система координат, но и другие системы координат - сферическая, цилиндрическая и т.д. Так как пространство трехмерное, в этих системах координат положение точки также будет определяться тремя изменяющимися во времени кинематическими параметрами.

Естественный способ. Он используется, когда траектория точки известна. Положение точки на траектории определяется примерно так же, как определяется положение числа на числовой оси.

Для этого нужно задать: 1) начало отсчета O₁; 2) положительное направление отсчета +; тогда положение точки M на траектории будет определяться 3) дуговой координатой s (рис. 57).

При движении точки M по траектории дуговая координата s изменяется с течением времени, то есть

s = s(t)

(4)

Выражение (4) определяет закон движения точки и является ее кинематическим уравнением движения в естественной форме.

Нельзя путать дуговую координату с длиной пути точки. Дуговая координата s может быть положительной, как показано на рис. 57, может быть равна нулю в начале отсчета и может быть отрицательной, когда точка перейдет за начало отсчета.

Путь, пройденный точкой, всегда положителен, так как он равен сумме всех перемещений точки за конечный промежуток времени, и не зависит ни от начала отсчета, ни от направления отсчета. Например, при движении точки по траектории из начала отсчета в положение M и назад дуговая координата точки равна 0, а путь равен 2s.

Связь между способами задания движения точки. Все три способа задания движения точки связаны между собой.

Найдем связь между координатным и векторным способами задания движения. Из математики известно, что координаты точки M являются проекциями ее радиус-вектора на оси системы координат. Записав радиус-вектор в координатной форме, выражаем эту связь:

(5)

где i,j,k являются единичными векторами (ортами) осей координат (рис. 57).

Рассмотрим переход от координатного способа задания движения к естественному. Выделим на траектории точки элементарное дуговое перемещение (дифференциал дуговой координаты) ds (рис. 57). Оно представляет собой диагональ прямоугольного параллелепипеда со сторонами dx, dy, dz, являющимися элементарными приращениями прямоугольных координат (дифференциалами этих координат). Величина диагонали ds равна

(6)

Обозначая производные по времени от координат

(7)

выражаем их дифференциалы: dx = xdt; dy = ydt; dz = zdt. Подставляя последние равенства в выражение (6), получаем

(8)

Предполагая, что при t = 0 точка находится в начале отсчета (s = 0), интегрируя выражение (7) в интервалах от 0 до s и от 0 до t, находим закон движения точки вдоль траектории:

Дата добавления: 2015-09-04