Элементарные звенья и их характеристики

Как известно из курса алгебры, полином произвольного порядка можно разложить на элементарные (простые) множители вида k, s,(s + ),(s ² + ). Поэтому любую дробно-рациональную передаточную функцию всегда можно представить в виде произве­дения элементарных множителей и элементарных дробей вида 1/ s, , .

Звенья, передаточные функции которых имеют вид элементар­ных множителей или элементарных дробей, называют элементар­ными. Элементарные множители, представляющие собой полиномы первого и второго порядка, можно преобразовать к принятому в тео­рии автоматического управления стандартному виду:

, , .

При этом k (k > 0) называют передаточным коэффициентом, Т (Т > 0) — постоянной времени (имеет единицу измерения вре­мени), — коэффициентом демпфирования.

Напомним правило вычисления модуля и аргумента дроби и произведения комплексных чисел, так как оно часто используется при вычислении амплитудной и фазовой частотных функций. Мо­дуль произведения комплексных чисел равен произведению модулей, а аргумент — сумме аргументов его сомножителей. Модуль дроби равен отношению модуля числителя к модулю знаменателя, а аргу­мент — разности аргументов числителя и знаменателя.

Рассмотрим основные типы элементарных звеньев.

Пропорциональное звено — звено с передаточной функцией W (s) = k. Его частотные и временные функции:

, , , , ,

, , .

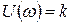Дифференцирующее звено — звено с передаточной функцией W (s) = ks. Его частотные и временные функции:

, , , , ,

, , .

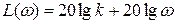Интегрирующее звено — звено с передаточной функцией W (s) = k/s. Его частотные и временные функции:

, , , , ,

, , .

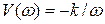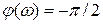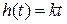Форсируюшее звено первого порядка — звено с передаточной функцией W (s) = k (Ts + 1). Его частотные и временные функции:

, , , , , , , .

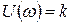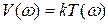Апериодическое звено — звено с передаточной функцией 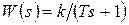. Его частотные и временные функции:

, , , ,

, , , .

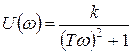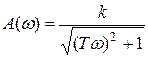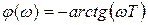Форсирующее звено второго порядка — звено с передаточной функцией , . Его частотные функции:

, , , ,

.

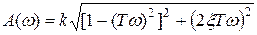Колебательное звено — звено с передаточной функцией . Его частотные и временные функции:

, , , ,

, ,

где , , .

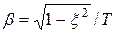При 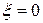это звено также называют консервативным.

Элементарные звенья относятся к типовым. Поэтому их также называют типовыми. Примером типового звена, не являющегося элементарным, является звено чистого запаздывания.

Звено чистого запаздывания — звено с передаточной функцией . Его частотные и временные функции:

, , , , , , , .

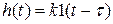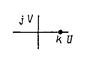
Звено и ее частотная передаточная функция	Амплитудно – фазоваячастотная характеристика	Логарифмические амплитудные и фазовые частотные характеристики
Пропорциональное звено
Дифференцирующее звено
Интегрирующее звено
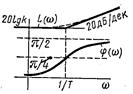
Форсирующее звено
Апериодическое звено
Колебательное звено

Дата добавления: 2015-09-04