
Читайте также:
|
Для аналитического исследования и математического моделирования ударно–вибрационных машин с двумя степенями свободы необходима разработка их расчетных схем. Расчетные схемы строят на основе общепринятых упрощений и допущений. Это является обычным для большинства прикладных задач теории колебаний. Инерционные тела, считают абсолютно твердыми телами. Одно из них является рабочим органом машины и взаимодействует с обрабатываемой средой. Влияние этой среды на динамику вибрационной машины будем учитывать присоединением к рабочему органу массы обрабатываемого материала и введением сопротивления. Сопротивление имитирует диссипацию энергии в обрабатываемой среде.
Такое допущение является приемлемым для изучения интересующих нас фазовых соотношений [18]. Массой упругих элементов, из-за их малости по сравнению с сосредоточенными массами тел будем пренебрегать [15]. Движение абсолютно твердых тел массами m1 и m2 будем считать прямолинейным возвратно поступательным.
Для негармонических колебаний рабочего органа в резонансных вибрационных машинах необходимы нелинейные упругие связи. Это нужно для обеспечения технологической устойчивости. В частности, для стабильности динамических характеристик, при изменении массы технологической нагрузки в сравнительно широких пределах. Комбинация постоянных упругих связей с упругими ограничителями хода (демпферами) позволяют получать разнообразные характеристики. Связи таких типов получим наиболее широкое распространение в конструкциях резонансных вибрационных машин. Характеристики таких упругих связей можно с достаточной точностью считать кусочно-линейными.
При исследовании колебаний упругой системы в области резонанса очень важен учет рассеяния энергии в упругих элементах. Внутреннее трение определяется рядом факторов. Влияние этих факторов весьма сложно. Наиболее распространение получила гипотеза Кельвина – Фойгта, которую часто называют гипотезой вязкого трения. Согласно гипотезе вязкого трения, диссипативная сила прямо пропорциональна деформации упругих связей. Следовательно, гипотеза вязкого трения при сравнительной простоте обеспечивает необходимое соответствие с экспериментальными данными [15], [16].
Всякий реальный источник энергии имеет ограниченную мощность [24]. Однако в нашем исследовании приводные электродвигатели имеют заметный запас мощности. Кроме того рассматриваться будут лишь стационарные колебания систем. Поэтому с достаточной для целей нашего исследования достоверностью можно считать, что рассматриваемые системы обладают источником энергии, неограниченным по мощности. Иными словами, можно считать угловую частоту вынуждающей силы постоянной.
На основании исследований весь класс двухмассных ударно – вибрационных машин с упругими ограничителями будем схематизировать в виде кусочно-линейных систем. При такой схематизации часть движения (когда нет удара) на рабочий орган и раму, либо вообще не действуют упругие силы, либо эти силы малы. Это объясняется деформацией упругих элементов малой жесткости, которые постоянно связывают два тела совершающих колебания. В момент удара, когда происходит соприкосновение двух тел, начинают действовать значительные упругие силы. Эти силы определяются деформацией упругих ограничителей с большими коэффициентами жесткости. Таким образом, при работе таких машин в течении одного периода движения суммарный коэффициент жесткости упругих связей меняется. Такой схемой может быть представлена большая группа распространенных ударно-вибрационных площадок для уплотнения бетонных смесей, виброгрохотов и некоторых других вибрационных машин.
Расчетные схемы ударно-вибрационных систем с центробежным и с эксцентриково-шатунным приводами, описывающие данный характер движения представлены на (рис. 5 и 6).

Рис. 5 Модели ударно-вибрационной системы с центробежным приводом

Рис. 6 Модели ударно-вибрационной системы
с эксцентриково-шатунным приводом.
Будем считать, что характеристики постоянных упругих элементов, резиновых ограничителей и опорных упругих элементов линейны. Диссипативное сопротивление, обусловленное наличием обрабатываемой среды, также примем пропорциональным скорости перемещения рабочего органа. Введем следующие обозначения:
m1 – масса уравновешивающей рамы;
m2 - масса рабочего органа, с присоединенной массой обрабатываемой среды;
С0, С1, С2, С3 - соответственно коэффициенты жесткости опорных пружин, упругих элементов постоянной подвески массы m1 и m2, упругого ограничителя и упругого элемента шатуна;
b, b0, b2 - соответственно коэффициенты сопротивления обрабатываемой среды, опорных элементов и упругого ограничителя;
e - радиус кривошипа с упругим шатуном;
 - угловая частота вынуждающей силы;
- угловая частота вынуждающей силы;
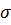 - ускорение свободного падения.
- ускорение свободного падения.
Введем систему отсчета, ось x направим вертикально вверх. Перемещение массы m1 обозначим через x1 и будем отсчитывать его от положения статического равновесия, при котором опорные пружины деформированы на величину  . Перемещение x2 массы m2 будем отсчитывать от этого же положения с добавлением недеформированной высоты пружин с коэффициентом жесткости С1. Следовательно, деформация пружин с коэффициентом жесткости С1 выражается, как x2 -x1. Деформация упругого ограничителя равна
. Перемещение x2 массы m2 будем отсчитывать от этого же положения с добавлением недеформированной высоты пружин с коэффициентом жесткости С1. Следовательно, деформация пружин с коэффициентом жесткости С1 выражается, как x2 -x1. Деформация упругого ограничителя равна 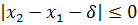 .
.
2.2 Динамика ударно-вибрационной системы с двумя степенями свободы, на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами
Уравнение движения ударно-вибрационной площадки с двумя степенями свободы имеет различный вид в зависимости от того, включился или не включился упругий ограничитель.
Для расчетной схемы ударно-вибрационной площадки с центробежным приводом (рис. 5), дифференциальные уравнения движения будут иметь вид:
 (25)
(25)
при 
 (26)
(26)
при 
Точкой обозначено дифференцирование по времени.
Для расчетной схемы с эксцентриково-шатунным приводом (рис. 6), дифференциальные уравнения движения будем иметь вид:
 (27)
(27)
при 
 (28)
(28)
при 
Точкой обозначено дифференцирование по времени.
Как уже отмечалось, такие системы называют кусочно-линейными. Движение кусочно-линейной системы состоит из чередующихся этапов. На каждом из этих этапов движение системы описывается линейными дифференциальными уравнениями. При изучении динамики ударно-вибрационных машин интерес представляют периодические движения. В реальных системах такие движения быстро устанавливаются благодаря наличию больших диссипативных сопротивлений. Параметры периодических движений - размах колебаний, экстремальные значения ускорений, фазовые соотношения, являются основными характеристиками таких машин.
Однако аналитическое определение даже простейших периодических решений для кусочно-линейных систем (в нашем случае с одним ударом об ограничитель за один период вынуждающей силы) очень затруднено.
Обычно применяемый для этих целей метод припасовывания [17] приводит к сложным трансцендентным уравнениям, выражающим условия периодичности. Кроме того, он требует предварительного построения последовательности этапов, а также исследования существования устойчивости полученного результата.
Приближенные методы, например метод гармонического баланса [17], дает недостаточную информацию, а также требует громоздких вычислений. Границы их применимости четко не устанавливаются.
Практически наиболее удобным способом нахождения периодических нелинейных движений, в частности кусочно-линейных систем, является математическое моделирование. Численное интегрирование дифференциальных уравнений движения с помощью компьютерного моделирования с последующим выделением периодического движения автоматически собирает устойчивые решения и позволяет найти все необходимые характеристики.
Для исследования одноударных периодических режимов вибрационных машин разработана компьютерная программа. Программа осуществляет численное интегрирование кусочно-линейных уравнений (25), (26) выделяет одноударные периодические решения и вычисляет параметры периодического движения схемы.
На (рис. 7), представлена блок-схема программы расчета периодических движений для двухмассной ударно-вибрационной системы.

Рис. 7 Блок-схема программы расчета периодических движений
Следующий блок осуществляет преобразования, необходимые для приведения уравнений к единому виду. Вводятся безразмерные переменные - время и перемещение. Тем самым устраняется возможная проблема разно масштабности переменных. Далее задаются стандартные начальные условия, соответствующие наличию положительного расстояния между массами  и
и  и параметры, необходимые для начала интегрирования.
и параметры, необходимые для начала интегрирования.
Численное интегрирование уравнений движения производится при помощи программы, реализующей метод Адамса - переменного шага и порядка [26]. Шаг интегрирования автоматически выбирается максимально возможным, исходя из заданной точности и текущего состояния системы, что обеспечивает высокую эффективность метода.
Возможны два типа движения масс  и
и  , раздельные и совместные. Тип движения определяется законом относительного перемещения:
, раздельные и совместные. Тип движения определяется законом относительного перемещения:

(29)
После каждого шага интегрирования вычисляется  . Если на выполненном шаге знак этой величины изменяется, то производится интерполяционное уточнение момента смены знака и вычисление состояния системы (то есть координат и скоростей), соответствующего этому моменту. После чего интегрирование продолжается, но уже для нового типа движения. Для интерполяции используется подпрограмма INTRP [26].
. Если на выполненном шаге знак этой величины изменяется, то производится интерполяционное уточнение момента смены знака и вычисление состояния системы (то есть координат и скоростей), соответствующего этому моменту. После чего интегрирование продолжается, но уже для нового типа движения. Для интерполяции используется подпрограмма INTRP [26].
Задачей расчета является определение параметров периодического движения системы с периодом  . Поэтому после каждого шага проверяется условие
. Поэтому после каждого шага проверяется условие  , где t - текущее значение времени.
, где t - текущее значение времени.
Если оно выполнено, то производится интерполяционное уточнение состояния в момент  (с помощью той же программы INTRP) и сравниваются состояния при t=0 и
(с помощью той же программы INTRP) и сравниваются состояния при t=0 и  С этой вычисляется величина:
С этой вычисляется величина:
 (30)
(30)
При  , где
, где 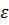 - заданное малое число, w - максимальное значение модуля фазовых координат за время интегрирования, периодическое решение считается достигнутым. В противном случае состояние при
- заданное малое число, w - максимальное значение модуля фазовых координат за время интегрирования, периодическое решение считается достигнутым. В противном случае состояние при 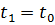 принимается в качестве начального и процесс повторяется.
принимается в качестве начального и процесс повторяется.
При достижении периодического решения полученные значения перемещений и скоростей на протяжении цикла переводятся в различные величины (м, м/с) и выводятся на печать вместе со значением времени (фазовых углов wt). В той же таблице приводятся относительное перемещение двух масс, кроме этого приводятся моменты перехода от раздельного движения к совместному ( ) и обратно (
) и обратно ( ); мощность, затрачиваемая на колебания при периодическом движении.
); мощность, затрачиваемая на колебания при периодическом движении.
Периодическое решение определяется с заданной точностью 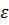 . В некоторых случаях (если абсолютное значение
. В некоторых случаях (если абсолютное значение  велико) принятой точности может оказаться недостаточно. Тогда следует уменьшить
велико) принятой точности может оказаться недостаточно. Тогда следует уменьшить 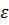 (рекомендуемые значения
(рекомендуемые значения  ). С другой стороны, уменьшение
). С другой стороны, уменьшение 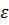 приводит к росту числа цикла, необходимого для установления периодического решения, то есть к увеличению продолжительности интегрирования. Рекомендуется при проведении расчетов эмпирическим путем подобрать наиболее подходящее значение
приводит к росту числа цикла, необходимого для установления периодического решения, то есть к увеличению продолжительности интегрирования. Рекомендуется при проведении расчетов эмпирическим путем подобрать наиболее подходящее значение 
При заданной частоте удара и массе рабочего органа эффективность ударно-вибрационной машины определяется ударной скоростью [17]. Поскольку машина является резонансной, максимальная (резонансная) ударная скорость достигается лишь при конкретных значениях основных параметров.
Для исследования расчетной модели при 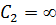 в соответствии с [8]. Относительная ударная скорость будет иметь вид:
в соответствии с [8]. Относительная ударная скорость будет иметь вид:

Отсюда видно, что относительная ударная скорость  имеет максимальное значение при
имеет максимальное значение при  то есть
то есть  Ф – фаза относительной ударной скорости.
Ф – фаза относительной ударной скорости.

где R – коэффициент восстановления скорости 
a, b- коэффициенты, определяющиеся из исходных данных параметров системы;
 максимальная относительная ударная скорость. Эта скорость достигается при оптимальной фазе вынуждающей силы
максимальная относительная ударная скорость. Эта скорость достигается при оптимальной фазе вынуждающей силы 

Из выражения (25) следует, что для режимов с максимальной относительной ударной скоростью, фаза равна  или фаза вынуждающей силы в момент удара равна
или фаза вынуждающей силы в момент удара равна  . Причем независимо от значения параметров, при которых достигнут максимум относительной ударной скорости и от величины этого максимума.
. Причем независимо от значения параметров, при которых достигнут максимум относительной ударной скорости и от величины этого максимума.
Данный результат получен для идеализированной системы 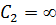 , чего в действительности не может быть.
, чего в действительности не может быть.
При 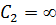 , то есть для линейной системы, результаты исследований изложены в работах [5], [17]. Фаза вынуждающей силы в момент удара равна
, то есть для линейной системы, результаты исследований изложены в работах [5], [17]. Фаза вынуждающей силы в момент удара равна  . В линейной системе за момент удара условно принимают момент перехода системы через положение равновесия.
. В линейной системе за момент удара условно принимают момент перехода системы через положение равновесия.
Таким образом, при изменении  от 0 до
от 0 до  в системах с одной степенью свободы значения фазы вынуждающей силы изменяются от
в системах с одной степенью свободы значения фазы вынуждающей силы изменяются от 
Для систем с двумя степенями свободы обозначим  - фазовый угол, соответствующий фазовому углу ударной скорости в момент сопротивления
- фазовый угол, соответствующий фазовому углу ударной скорости в момент сопротивления 
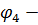 фазовый угол в момент отрыва
фазовый угол в момент отрыва  фазовый угол в момент перехода скорости через нуль. Согласно принятому отчету при
фазовый угол в момент перехода скорости через нуль. Согласно принятому отчету при
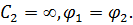
Для двухмассной ударно-вибрационной установки с эксцентриково-шатунным приводом применим следующие рассуждения.
В следующем блоке осуществляется преобразования, необходимые для приведения уравнений к единому виду. Вводятся безразмерные переменные – время и перемещение. Далее задаются стандартные начальные условия, соответствующие наличию положительного расстояния между массами m1 и m2 и параметры, необходимые для начала интегрирования.
Тип движения определяется знаком относительного перемещения:
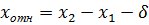 . (34)
. (34)
2.3 Анализ результатов исследования динамики вибрационной системы с двумя степенями свободы, на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами.
Исследование двухмассных ударно-вибрационных машин с центробежным приводом, дают возможность построить зависимости ускорения  рабочего органа
рабочего органа  ускорения
ускорения 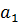 активной массы
активной массы  и угла сдвига фаз
и угла сдвига фаз  между вынуждающей силой и переходом относительной скорости через нуль и максимум ускорений от частоты вынуждающей силы
между вынуждающей силой и переходом относительной скорости через нуль и максимум ускорений от частоты вынуждающей силы  .
.
Максимумы ускорений масс 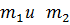 совпадают с моментом перехода относительной скорости через нуль.
совпадают с моментом перехода относительной скорости через нуль.
На (рис. 8, 9, 10) приведены зависимости  и
и  для машин с центробежным приводом. Зависимости соответствуют постоянным значениям:
для машин с центробежным приводом. Зависимости соответствуют постоянным значениям:  ,
, 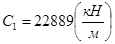 ,
,  ,
,  ,
,  ,
,  ,
,  . При этом соотношение
. При этом соотношение  . Из этих зависимостей видно, что при изменении
. Из этих зависимостей видно, что при изменении  от 8000 кг до 13000 кг, угол
от 8000 кг до 13000 кг, угол  в резонансном режиме изменяется от 3,5 рад до 3,17 рад.
в резонансном режиме изменяется от 3,5 рад до 3,17 рад.
Из графиков на (рис. 8) видно, что в диапазоне  от 5850 кг до 10000 кг;
от 5850 кг до 10000 кг;  от 2860 кг до 10000 кг; RM от 2,33 до 2,88 кг;
от 2860 кг до 10000 кг; RM от 2,33 до 2,88 кг;  от 13792 до 22889
от 13792 до 22889 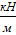 ;
; 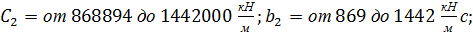
 от 120 до 132
от 120 до 132  ;
;  от -0,00256 м до -0,00725 м при сохранении постоянства
от -0,00256 м до -0,00725 м при сохранении постоянства  при резонансе.
при резонансе.
Зависимости на (рис. 9), соответствуют значениям 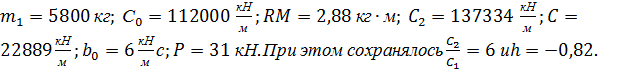
Отрицательный зазор в этом случае достигается за счет силы постоянного поджатия Р. Из графиков на (рис. 10) видно, что в диапазоне  от 8000 кг до 13000 кг и b от 96
от 8000 кг до 13000 кг и b от 96 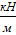 с до 156
с до 156  угол
угол 

Рис. 8 График зависимости 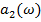 и
и  для систем с центробежным приводом при
для систем с центробежным приводом при 
Кривые 1,1 при 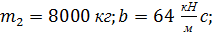
Кривые 2,2 при  10000 кг;
10000 кг; 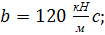
Кривые 3,3 при 

Рис. 9 График зависимости 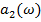 и
и  для систем с центробежным приводом при h=0 и
для систем с центробежным приводом при h=0 и 
Кривые 1,1е при 
Кривые 2,2е при 
Кривые 3,3е при 

Рис. 10 График зависимости  для систем с центробежным приводом при
для систем с центробежным приводом при
h= - 0,82 и 
Кривые 1, I при 
Кривые 2, II при 
Кривые 3,III при 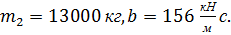
Приведенные зависимости наглядно показывают, что угол  в основном при резонансе зависит от отношений
в основном при резонансе зависит от отношений  и ударного зазора h и не зависит от других параметров системы (
и ударного зазора h и не зависит от других параметров системы ( ). Изменения, которых неизбежны в процессе эксплуатации машины. Действительно из графиков следует, что в широком диапазоне изменения выше указанных параметров при соблюдении постоянства
). Изменения, которых неизбежны в процессе эксплуатации машины. Действительно из графиков следует, что в широком диапазоне изменения выше указанных параметров при соблюдении постоянства  Фазовый угол не изменяется и равен 3,09 рад. При
Фазовый угол не изменяется и равен 3,09 рад. При  в широком диапазоне изменения прочих параметров,
в широком диапазоне изменения прочих параметров,  Однако при таком же соотношении
Однако при таком же соотношении  на отрицательном зазоре h= - 0,82 мм, который получен за счет предварительного поджатия Р=32 кН, угол
на отрицательном зазоре h= - 0,82 мм, который получен за счет предварительного поджатия Р=32 кН, угол  оказывается равным 3 рад.
оказывается равным 3 рад.
Из изложенного вытекает, что в двухмасных вибрационных машинах с упругими ограничителями, фазовый угол  зависит от отношения коэффициентов жесткости
зависит от отношения коэффициентов жесткости  и ударного зазора h и не зависит от прочих параметров, изменяющихся в процессе работы.
и ударного зазора h и не зависит от прочих параметров, изменяющихся в процессе работы.
Далее были изучены резонансные режимы работы при других соотношениях  ,
,  Результаты этих исследований в виде зависимостей
Результаты этих исследований в виде зависимостей 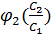 приведены на (рис. 9, 10). Зависимости на (рис.. 9, 10) полностью подтвердили, что при резонансном режиме работы фазовый угол
приведены на (рис. 9, 10). Зависимости на (рис.. 9, 10) полностью подтвердили, что при резонансном режиме работы фазовый угол  зависит только от соотношения
зависит только от соотношения  и величины зазора h. Иначе говоря, этот при поддержании h=const постоянен для каждой конкретной машины. Итоги расчета установившихся колебаний виброплощадки с центробежным приводом в резонансном режиме работы машины имеет вид:
и величины зазора h. Иначе говоря, этот при поддержании h=const постоянен для каждой конкретной машины. Итоги расчета установившихся колебаний виброплощадки с центробежным приводом в резонансном режиме работы машины имеет вид:

| 
| |
| Масса, кг |

| 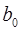
| 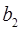
| |
| Коэффициенты демпфирования, кН*с/м |

| 
| 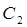
| |
| Коэффициенты жесткости, кН/м |
| Частота вынуждающего воздействия, рад/с | |
Момент масс дебаланса, кг 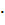 м м
| 2.333 |
| Зазор при недеформированных пружинах, м | 0.07 |
| Предварительное натяжение пружин, кН | |
| Шаг частоты, рад/с | |
| Число шагов | |
| Ошибка вычисления периодического решения | 0.000100 |
| ТРМ=6.199Е+00 ТРМ=1.230Е+00 | |||
| Максимальное перемещение m1 | -0.00282 м | Фаза | 0.593 
|
| Минимальное перемещение m1 | -0.00237м | Фаза | 3.962 
|
| Максимальное перемещение m2 | -0.0391 м | Фаза | 3.787 
|
| Минимальное перемещение m2 | -0.00504 м | Фаза | 0.506 
|
| Максимальное ускорение m1 | 5.07886 G | Фаза | 4.346 
|
| Минимальное ускорение m1 | -23.96047 G | Фаза | 0.506 
|
| Максимальное ускорение m2 | -6.60999 G | Фаза | 0.471 
|
| Минимальное ускорение m2 | -2.00506G | Фаза | 4.154 
|
| Мощность, затрачиваемая на колебания | 31.32184 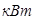
| ||
| Число циклов |

Рис. 11 График зависимости  для h = 0 (кривая 1), h = 2 мм (кривая 2) с центробежным приводом.
для h = 0 (кривая 1), h = 2 мм (кривая 2) с центробежным приводом.
Исследования динамики двух массных ударно – вибрационных машин с упругими ограничителями с эксцентриково – шатунным приводом дает возможность построить зависимости ускорения a2 рабочего органа m2; ускорения a1 активной массы m1 и угла сдвига фаз вынуждающей силой и переходом относительной скорости через нуль и максимумом ускорений от частоты вынуждающей силы  .
.
Максимумы ускорений масс m1 и m2 совпадают с моментом перехода относительной скорости через нуль.
На (рис. 12, 13) приведены зависимости  и
и  для машин с эксцентриково – шатунным приводом.
для машин с эксцентриково – шатунным приводом.
На (рис. 12), зависимости соответствуют: 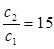 ;
;  ;
;  ;
;  ;
; 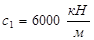 ;
;  ;
; 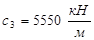 ;
;  ;
;  ;
;  . Из этого вытекает, что при эксцентриково-шатунном приводе, при изменении m2 от 6000 кг до 9600 кг; b от
. Из этого вытекает, что при эксцентриково-шатунном приводе, при изменении m2 от 6000 кг до 9600 кг; b от  до
до  ;
;  постоянен в резонансном режиме работы.
постоянен в резонансном режиме работы.
Другой график приведен на (рис. 13). Из этих графиков видно, что в диапазоне изменения m2 от 7800 кг до 12000 кг; m1 от 7800 кг до 10000 кг; e от 0.016 м до 0.021 м; bот  до
до  ;
;  ;
;  до
до  и при сохранении постоянства h=0,
и при сохранении постоянства h=0,  ;
; 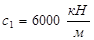 ;
; 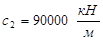 ; угол
; угол  при резонансе.
при резонансе.

Рис. 12 График зависимости 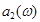 и
и  для системы с эксцентриково – шатунным приводом при
для системы с эксцентриково – шатунным приводом при 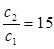 ;
; 
Кривые 1, 1bпри m2=6000кг; 
Кривые 2, 2bпри m2=7200кг; 
Кривые 3, 3bпри m2=9600кг; 

Рис. 13 График зависимости 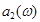 и
и  для системы с эксцентриково – шатунным приводом при
для системы с эксцентриково – шатунным приводом при 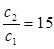 ;
; 
Кривые 1, 1c при m1=7800кг; m2=10000 кг; e=0.021 м;  ;
;  ;
; 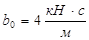 ;
; 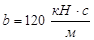 .
.
Кривые 2, 2c при m1=7800 кг; m2=12000 кг; e=0.021 м;  ;
;  ;
; 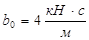 ;
;  .
.
Кривые 3, 3c при m1=10000кг;m2=7800кг; e=0.016м;  ;
;  ;
;  ;
; 
Приведенные зависимости наглядно показывают, что угол  в основном при резонансе зависит от отношения
в основном при резонансе зависит от отношения  и ударного зазора h и не зависит от других параметров системы (m1, m2, b, b2, b0). Изменения, которые неизбежны в процессе эксплуатации машины. Действительно из графиков следует, что в широком диапазоне изменения указанных выше параметров при соблюдении постоянства
и ударного зазора h и не зависит от других параметров системы (m1, m2, b, b2, b0). Изменения, которые неизбежны в процессе эксплуатации машины. Действительно из графиков следует, что в широком диапазоне изменения указанных выше параметров при соблюдении постоянства  и h=0. Фазовый угол не изменяется и равен
и h=0. Фазовый угол не изменяется и равен  . При
. При  и h=2мм в широком диапазоне изменения прочих параметров,
и h=2мм в широком диапазоне изменения прочих параметров,  . Однако при таком же отношении
. Однако при таком же отношении  , но отрицательном зазоре h=-0.82мм который получен за счет предварительного поджатия P=32кН, угол
, но отрицательном зазоре h=-0.82мм который получен за счет предварительного поджатия P=32кН, угол  оказывается равным
оказывается равным  .
.
Из изложенного выше, что в двух массных ударно – вибрационных машинах с упругими ограничителями, фазовый угол  зависит от отклонения коэффициентов жесткости
зависит от отклонения коэффициентов жесткости  и удельного зазора h и не зависит от прямых параметров, изменяющихся в процессе работы.
и удельного зазора h и не зависит от прямых параметров, изменяющихся в процессе работы.
Далее были изучены резонансные режимы работы при других соотношениях  , m1, m2, b, b2, b0. Результаты этих исследований в виде зависимости
, m1, m2, b, b2, b0. Результаты этих исследований в виде зависимости  приведены на рисунке 11.
приведены на рисунке 11.
Зависимость на (рис. 11) полностью подтвердила, что при резонансном режиме работы машины фазовый угол  зависит только он соотношения
зависит только он соотношения  и величины зазора h. Иначе говоря, этот угол при поддержании h=const постоянен для каждой конкретной машины. Распечатка расчета установившихся колебаний виброплощадки с эксцентриково – шатунным приводов в резонансном режиме работы машины имеет вид:
и величины зазора h. Иначе говоря, этот угол при поддержании h=const постоянен для каждой конкретной машины. Распечатка расчета установившихся колебаний виброплощадки с эксцентриково – шатунным приводов в резонансном режиме работы машины имеет вид:
| m1 | m2 | |
| Масса, кг |
| B | b0 | b2 | |
Коэффициент демпфирования,

|
| c0 | c1 | c2 | |
| Коэффициент жесткости, кН / м |
Частота вынужденного воздействия, 
| |
Радиус кривошипа, 
| 0.16 |
Зазор при недеформированных пружинах, 
| 0.013 |
Шаг частоты, 
| 0.0001 |
| Число шагов | |
| Ошибка вычисления периодического решения | 0.0000500 |
| ТРМ=6.199Е+00 ТРМ=1.230Е+00 | |||
| Максимальное перемещение m1 | 0.1007 
| Фаза | 0.593 
|
| Минимальное перемещение m1 | -0.0779 
| Фаза | 3.962 
|
| Максимальное перемещение m2 | 0.00974 
| Фаза | 3.787 
|
| Минимальное перемещение m2 | -0.01053 
| Фаза | 0.506 
|
| Максимальное ускорение m1 | 2.67953 
| Фаза | 4.346 
|
| Минимальное ускорение m1 | -8.322386 
| Фаза | 0.506 
|
| Максимальное ускорение m2 | 10.11375 
| Фаза | 0.471 
|
| Минимальное ускорение m2 | -2.78398 
| Фаза | 4.154 
|
| Мощность, затрачиваемая на колебания | 31.32184 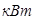
| ||
| Число циклов |

Рис. 14 График зависимости  для системы с эксцентриково-шатунным приводом при;
для системы с эксцентриково-шатунным приводом при;  (кривая 1);
(кривая 1);  (кривая 2)
(кривая 2)
2.4 Выводы по разделу
1. Предложены упрощенные математические модели двухмассных ударно-вибрационных машин с упругими ограничителями с центробежным приводом и с эксцентриково-шатунным приводом.
2. Разработка программы расчета двух массных ударно вибрационных машин, позволяющая находить их основные параметры и фазовые соотношения.
3. Установлена закономерность для всех двухмассных ударно-вибрационных машин с упругими ограничителями, состоящая в том, что при резонансном режиме работы фазовые углы 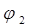 между вынуждающей силой и переходом скорости через нуль зависит только от соотношения коэффициентов жесткости упругих ограничителей и постоянных упругих связей и величины зазора.
между вынуждающей силой и переходом скорости через нуль зависит только от соотношения коэффициентов жесткости упругих ограничителей и постоянных упругих связей и величины зазора.
4. Найденные зависимости дает возможность использовать систему автоматического фазового регулирования по выбору фазовых углов 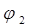 в зависимости от соотношения
в зависимости от соотношения  и зазора h.
и зазора h.
3. МЕТОДИКА РАСЧЕТА ДВУХМАССНОЙ РЕЗОНАНСНОЙ УДАРНО-ВИБРАЦИОННОЙ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
3.1 Расчет резонансной ударно-вибрационной системы с двумя степенями свободы, на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами.
Для двухмассной ударно-вибрационной виброплощадки с центробежным приводом исходными данными при резонансе являются:
 масса рабочего органа;
масса рабочего органа;
 частота вынуждающей силы;
частота вынуждающей силы;
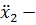 максимальное ускорение рабочего органа.
максимальное ускорение рабочего органа.
Целесообразно предварительно используя результаты приближенных исследований системы уравнений, определить значения  и
и 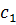 – жесткости основных упругих элементов и ограничителя; S – статический момент массы дебаланса;
– жесткости основных упругих элементов и ограничителя; S – статический момент массы дебаланса;  масса первого тела.
масса первого тела.
Согласно [15] расчет производных производим в следующем порядке:
1. На основе опыта конфигурирования и эксплуатации машин принимаем 
2. Жесткость постоянных упругих связей:
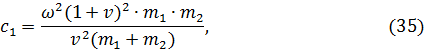
где  собственная частота колебаний системы с
собственная частота колебаний системы с
упругими связями,  приведенная масса системы;
приведенная масса системы;
 собственная частота колебаний с суммарной жесткостью упругих связей
собственная частота колебаний с суммарной жесткостью упругих связей 
3. Жесткость упругих ограничителей:

4. Максимальная деформация упругих ограничителей:

5. Используя прямую линеаризацию, находим статический момент массы дебалансов (кг 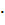 м), при котором выдерживается принятое значение
м), при котором выдерживается принятое значение 
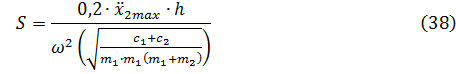
6. Считая, что рассеивание мощности происходит только в той части периода движения, когда деформирован упругий ограничитель, мощность необходимая для поддержания колебаний в системе соответствует:

где h – коэффициент затухания; h = (0,8  )
) 
7. Мощность приводного электродвигателя:

где 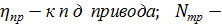 мощность затрачиваемая на трение:
мощность затрачиваемая на трение:

где  приведенный к валу коэффициент трения скольжения подшипника качения (при жидкой смазке), d – диаметр шейки вала под подшипником.
приведенный к валу коэффициент трения скольжения подшипника качения (при жидкой смазке), d – диаметр шейки вала под подшипником.
По выражениям для  задавшись числом упругих элементов и ограничителей, находят коэффициент жесткости одного элемента. Расчет резиновых ограничителей производят с учетом их максимальной деформации при ударе. По выражению для S, задавшись числом дебалансов, находят статический момент массы одного дебаланса. Далее определяют его геометрические размеры.
задавшись числом упругих элементов и ограничителей, находят коэффициент жесткости одного элемента. Расчет резиновых ограничителей производят с учетом их максимальной деформации при ударе. По выражению для S, задавшись числом дебалансов, находят статический момент массы одного дебаланса. Далее определяют его геометрические размеры.
При исследовании колебаний системы в области резонанса очень важен учет рассеяния энергии в упругих элементах.
Внутреннее трение определяется рядом факторов, влияние которых очень сложно. Наибольшее распространение получила гипотеза вязкого трения. Она предлагает, что диссипативные силы пропорциональны скорости деформации упругих связей. Рассеяние энергии в нелинейных упругих связях можно представить функцией:

где  кусочно – постоянная функция;
кусочно – постоянная функция;
 коэффициенты жесткости упругих связей.
коэффициенты жесткости упругих связей.

где h – зазор в буферах;  коэффициент внутренних сопротивлений, для резиновых ограничителей
коэффициент внутренних сопротивлений, для резиновых ограничителей 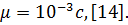 По рекомендации [18] рассеяние энергии в резиновых упругих связях в (2
По рекомендации [18] рассеяние энергии в резиновых упругих связях в (2 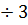 ) раза выше, чем остальных.
) раза выше, чем остальных.
После ориентировочного расчета основных параметров системы, можем провести уточнение их с использованием программы ASSVM.
Покажем на численном примере последовательность определения основных параметров двух массной ударно-вибрационной площадки. Известна масса рабочего органа  максимальное ускорение рабочего органа задано
максимальное ускорение рабочего органа задано 
Принимаем величину 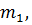 равной:
равной:

2. Жесткость постоянных упругих связей:


где  в соответствии с [11].
в соответствии с [11].
3. Жесткость упругих ограничителей:

4. Статический момент массы дебалансов:
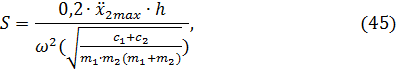


5. Значения коэффициентов сопротивлений принимаем по рекомендациям в работах [15], [17].
Суммарные значения коэффициента сопротивления упругих элементов постоянной подвески массы 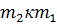 и обрабатываемой среды принимаем равным
и обрабатываемой среды принимаем равным 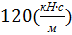 .
.
Имеем 
 .
.
Значения жесткостей опорных упругих элементов  принимается по условию их прочности,
принимается по условию их прочности, 
Будем проводить расчет машины с нулевым ударным зазором. При не деформированных пружинах с коэффициентом жесткости 
Используя программу, задавшись шагом  получаем данные для построения зависимостей
получаем данные для построения зависимостей 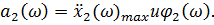
Эти зависимости показаны на (рис. 9, кривые 1,1е). Из графика видно, что резонанс достигается при частоте вынуждающей силы
 , то есть отклонение от предварительной заданной резонансной частоты составляет:
, то есть отклонение от предварительной заданной резонансной частоты составляет:

Фазовый угол 
Решение нелинейных дифференциальных уравнений, описывающих динамику машины с эксцентриково – шатунным приводом с упругими элементами в шатуне, осложняются тем, что они не интегрируемы в квадратурах. Поэтому приходится идти по пути широкого применения приближенных методов.
В данном методе при нахождении первого приближения осуществляется эквивалентная линеаризация. Причем частота собственных колебаний и декремент затухания линеаризованной системы являются функциями амплитуды периодической составляющей деформации основных упругих связей и амплитуды деформации приводов элементов.
Динамика резонансной ассиметричной вибрационной площадки, соответствующей расчетной схеме на (рис. 8), хорошо изучена[18]. Там же приведены методика расчета резонансных асимметричных вибрационных площадок, которая дает возможность выбрать параметры системы. Исходные данные для расчета таких машин являются:
а) предела изменения минимального ускорения  рабочего органа;
рабочего органа;
б) асимметрия закона движения рабочего органа

где  ,
,  - максимальные и минимальные ускорения рабочего органа;
- максимальные и минимальные ускорения рабочего органа;  - выбирается из технологических соображений
- выбирается из технологических соображений  ;
;
в) диапазон рабочих частот  вынуждающей силы;
вынуждающей силы;
г) масса рабочего органа  ;
;
Далее, руководствуясь [18], определим основные параметры вибрационной площадки:
1) масса  уравновешивающей рамы равно:
уравновешивающей рамы равно: 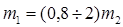 ;
;
2) коэффициенты формы колебаний:  ;
;
3) амплитуда  периодической составляющей деформации основных упругих связей связана с амплитудой
периодической составляющей деформации основных упругих связей связана с амплитудой  колебаний рабочего органа соотношением:
колебаний рабочего органа соотношением:
 ;
;
4) смещение центра колебаний относительного положения статического равновесия  при нулевом зазоре в буферах:
при нулевом зазоре в буферах:
 ,
,
где  ;
;
5) величина жесткости линейных основных упругих связей:
 ,
,
где,  - приведенная масса системы;
- приведенная масса системы;
6) жесткость упругого ограничителя определяется выражением:
 ;
;
7) эксцентриситет приведенного вала следует принимать:
 ;
;
8) частота вынуждающей силы определяется как:
 ,
,
для следующего случая нулевого зазора в буферах:
при  ,
,  , [18];
, [18];
9) жесткость опорных упругих элементов выбирается минимально возможной по условиям их прочности;
10) жесткость приводных упругих связей выбирается как:

где, 
Рассмотрим численный пример предварительного определения основных параметров двух массной вибрационной площадки.
Пусть нам известно:  ;
;  ;
;  ;
;  ;
;  .
.
1) примем значение 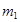
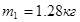 ;
;  .
.
2) коэффициент формы колебания определим по формуле:
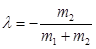 ;
;
 ;
;
3) приведены масса системы определения как:
 ;
;
 ;
;
4) амплитуда  периодической составляющей деформации основных упругих связей определяется соотношением:
периодической составляющей деформации основных упругих связей определяется соотношением:
 ;
;
 ;
;
5) смещение центра колебаний относительно положения статического равновесия для зазора в буферах найдем как:
 ,
,
 ;
;  ;
;
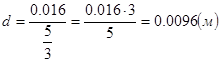 ;
;
6) жесткость линейных основных упругих связей будет равна:
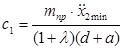 ;
;
 ;
;
7) жесткость ограничителя должна удовлетворять соотношению:
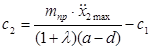 ;
;
 ;
;
8) эксцентриситет приводного вала примем равным:

9) частота вынуждающей силы:
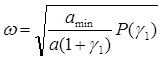 ;
;
 ;
;
где  - для нулевого зазора в буфере при
- для нулевого зазора в буфере при  равно:
равно:
 ,[18].
,[18].
10) жесткость приводных упругих связей выбирается как:
 ,
,
где  ,
, 
11)  -максимальная масса рабочего ор
-максимальная масса рабочего ор
Дата добавления: 2015-09-04; просмотров: 129 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Динамика резонансных ударно-вибрационных машин | | | Выводы по разделу |