Динамика резонансных ударно-вибрационных машин

При разработке резонансных вибромашин конструкторам приходится учитывать большое число разнообразных требований, предъявляемых современным производством к новой технике. Наиболее существенными и принципиальными являются следующие: реализация рабочих режимов, близких к оптимальным; простота машин и удобство в эксплуатации; высокая эксплуатационная надежность; минимальная энергоемкость формирования, соответствие оборудования современными санитарно-гигиеническим требованиям; машины должны легко вписываться в существующие и вновь создаваемые технологические линии.

Успешное выполнение этих условий в значительной степени определяется удачным выбором принципиальных схем вибромашин и, как следствие этого, их расчетных схем. Для уплотнения бетонных смесей необходимы различные законы колебаний в зависимости от направления движения рабочего органа. Так, при горизонтальных колебаниях, закон движения рабочего органа должен быть симметричным, а при вертикальных - асимметричным. Отсюда следует, что вибрационные машины с горизонтальными колебаниями рабочего органа могут иметь только симметричную упругую систему. В машинах с вертикальными колебаниями рабочего органа целесообразно применять упругие связи с асимметричной характеристикой восстанавливающей силы.

Принципиально возможно создавать машины с двух- и трех координатным движением рабочего органа, однако детальный анализ технологических преимуществ и особенностей таких рабочих режимов пока не проводится.

В процессе работы над резонансными вибромашинами уплотнения бетонных смесей были тщательно проанализированы специфические особенности поведения большого числа динамических схем. Оказалось, что рассмотренным выше условиями может удовлетворять сравнительно простые в конструктивном отношении двухмассные системы. При вертикальных колебаниях рабочего органа благодаря этим системам осуществляется эффективная виброизоляция, а при горизонтальных – реализуются динамически уравновешенные схемы с двумя рабочими органами. В последнем случае динамические усилия на основание вибромашин не передаются. Создание виброформовочных машин с числом основных движущихся масс больше двух нецелесообразно, практику это приводит к неоправданному усложнению динамических машин.

Всякий реальный источник энергии имеет ограниченную мощность, поэтому возникает необходимость учитывать процессы его взаимодействия с колебательной системой, особенно в резонансных вибромашинах. При составлении уравнений движения можно воспользоваться предложенным Кононенко В.О. [24] подходом, который основывается на использовании статических характеристик источников энергии при проведении динамических расчетов. В резонансных вибромашинах вращение на привод передаются обычно от асинхронных электродвигателей, статические характеристики которых хорошо изучены.

Наиболее сложным и наименее исследованным остается вопрос о характере взаимодействия машины с обрабатываемой средой. Однако при определении амплитудно-частотных характеристик вибромашины и решении задач синтеза можно учитывать влияние бетонной смеси как присоединенной массы и некоторого дополнительного затухания. Динамика резонансных асимметричных виброплощадок. Резонансные виброплощадки в динамическом отношении является двухмассными системами. Наличие двух основных движущихся масс позволяет соответсвующими подбором характеристик упругих свзязей решить две задачи: обеспечить необходимый закон движения рабочего ограна и создать эффективную виброизоляцию системы.

На (рис. 4) представлена схема резонансной асимметричной виброплощадки [6]. Между рабочим органом и уравновешивающей рамой устанавливаются буфера, соударяющиеся только при встречном движении масс и создающие билинейную упругую характеристику. При конструировании резонансных асимметричных виброплощадок были ипользованы динамические схемы с линейными и нелинейными характеристиками приводных упругих связей. В теоретическом отношении первый случай оказывается более простым, и ниже ограничимся его рассмотрением.

Рис. 4 Cхема резонансной асимметричной виброплощадки (1-рабочий орган с формой; 2-уравновешивающая рама; 3-кривошипно-шатунный привод; 4-приводной элемент; 5-буфер; 6-подрамный амортизатор)

Дифференциальные уравнения, описывающие колебания асимметричной виброплощадки, имеют вид:

;

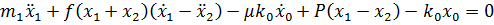(4)

где - масса рабочего органа;

- масса виброизолирующий рамы;

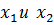- их абсолютные перемещения;

- жесткость приводных амортизаторов;

- жесткость опорных амотризаторов.

Характеристики основных упругих связей могут быть представлены в

виде:

(5)

(6)

(7)

где 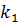- жесткость линейных основных упругих связей;

- жесткость упругих ограничителей хода (буферов);

Поскольку резонансные асимметричные виброплощадки работают в области основного резонанса, то для корректного использования метода Крылова-Боголюбова при построениии решения необходимо сделать дополнительные предположения о малости диссипативных сил ( и нелинейных членов:

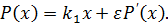(8)

Системы такого типа достаточно хорошо изучены. Амплитудно-частотное уравнение, получаемое с помощью метода Крылова-Боголюбова для первого приближения:

(9)

Рассматриваемая упругая система обладает двумя степенями свободы соответственно с двумя частотами собственных колебаний. Стремление к лучшей виброизоляции приводит к выбору упругих элементов с минимальной жесткостью в качестве опорных амортизаторов. Ограничения связаны только с обеспечением их прочности. Поэтому одна из частот собственных колебаний оказывается относительно низкой. В качестве рабочей принимают частоту, лежащую во второй резонасной области.

Отметим, что из системы уравнений (8) нетрудно получить уравнение вида (9):

(10)

Без заметного ущерба для точности получаемых решений в нем можно пренебречь диссипативным членом и в дальнейшим считать:

(11)

Рассматриваемая колеблющаяся система является асимметричной, поэтому асимметричными оказывается и периодические колебания, возникающие в этой системе. Если разложить такое решение в ряд Фурье, то в нем будут присутствовать наряду с нечетными и четные гармоники, в частности, могут появляться постоянные составляющие решения.

Первое приближение решения может быть представлено в виде:

(12)

Действительно, из уравнений (9) следует, что колебания масс происходят синфазно и в противофазе друг относительно друга (при пренебрежении рассеиванием энергии в опорных амортизаторах). Второе уравнение (12) справедливо только при Подставляя соотношения (9) в уравнение (8), определим,что

(13)

При малой жесткости опорных амортизаторов 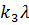в области рабочих частот колебания оказываются отрицательными. Следовательно, рабочие режимы резонансных виброплощадок связаны с противофазными колебаниями основных движущихся масс.

Из уравнения (10) следует, что для первого приближения решения выполняются соотношения:

(14)

которые будут использованы ниже. Отметим, что

Введем новую переменную

Тогда и первое из уравнений системы (3) можно привести к виду:

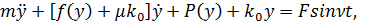(15)

где

В связи с производительностью выбора начальной фазы в законе изменения в правой части уравнения (11) принято, что возмущающая сила имеет нулевой фазовый угол.

При сделанных выше предположениях метод Крылова-Боголюбова позволяет найти соотношения, определяющие параметры первого приближения периодического решения:

(16)

Динамическое смещение центра колебаний асимметричной системы определяется в соответствии с работой [5] из условия равенства статических сил в уравнении (15):

(17)

где

Амплитудное и фазовое уравнения для основной гармоники имеют вид:

(18)

(19)

(20)

(21)

Момент сил сопротивления на ведущем валу:

(22)

где,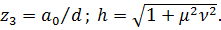

Для более полного анализа динамики асимметричных систем вновь обратимся к улучшенному первому приближению решения исходного уравнения (12). Параметры второй и третьей гармоник определяются следующими соотношениями:

(23)

Закон относительного движения масс можно представить в виде:

(24)

Специфическая особенность решения для асимметричных систем - появление четных гармоник в законе колебаний, что позволяет осуществить в виброплощадках рабочие режимы, близкие к оптимальным. Амплитуда второй гармоники и асимметрия закона движения зависит от жесткости буферов и установленного зазора и могут легко регулироваться. Ширина резонансной области в рассматриваемых асимметричных системах практически такая же, как и в линейных. Однако вопросы технологической устойчивости в резонансных виброплощадках с вертикальными колебаниями рабочего органа удается решать на базе выдвинутой идеи самоподстройки: параметры билинейной характеристики упругих связей подбираются так, что при увеличении массы рабочего органа, благодаря деформации линейных основных упругих связей и уменьшению зазора в буферах линеаризованная частота собственных колебаний системы остается практически постоянной.

Дата добавления: 2015-09-04