
|
Читайте также: |
Жүйе тербелістерінің өзіндік жиіліктерінің саны оның еркіндік дәрежесінің санына тең. Екі осьті автомобильдің тербелмелі жүйесінің төрт өзіндік жиіліктері болады.
Алдымен әсерді басу жоқ кезінде тек ғана рессорлы массаның тербелістерін қарастырамыз, яғни тербелістер сөнбейді деп қарастырамыз. Алдында және артында рессорлы масса жерге екі бір ізбен қосылған серпімді элементтер, яғни аспаның серпімді элементі (қаттылығы ср) және шина (қаттылығы сш) арқылы тіренеді.
Көрсетілген серпімді элементтерді бір элементпен алмастырамыз, сонда оның қаттылығы спр арнайы таңдалып алынады және спр келтірілген қаттылық деп аталады. Келтірілген қаттылық нақты тербелмелі жүйенің бірнеше серпімді элементтерін бір элементпен алмастырғанда кейбір күштің әсерімен туындайтын иілулер бірдей болу шартынан таңдалады.
Р күшінің әсер ету сызығына екі серпімді элемент қойылған (14.2-сурет).
Қаттылықтары сәйкес ср және сш болатын элементтердің иілулері:
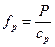 және
және 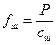 .
.
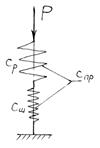
14.3-сурет – Серпімді элементтерді бір серпімді элементпен алмастыру.
осы күштің әсерімен бұл элементтердің жиынтық иілуі:
 .
.
иілу бірдей болу шартынан табатынымыз:
fnp= fp+ fш. (14.3)
осыдан
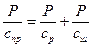 . (14.4)
. (14.4)
Немесе
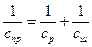 .
.
Ақырында
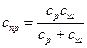 . (14.5)
. (14.5)
Көрсетілген қаттылықтарды пайдалана отырып және рессорсыз массаларды ескермей, екі еркіндік дәрежесі бар жүйені табамыз, сонда бұл жүйенің масса центрінің вертикаль жылжуы Ζ0 және бойлық жазықтықта бұрылуы α болады (14.3 – сурет).
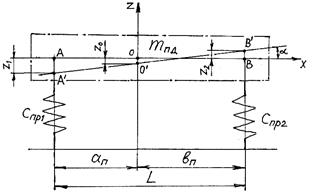
14.3-сурет – Екі еркіндік дәрежесі бар тербелмелі жүйе.
Бұл екі қозғалыс серпімді элементтердің Ζ1 және Ζ2 иілулерінің өзгерулеріне және осы элементтер жағынан рессорлы массаға әсер ететін серпімділік күштердің спр1Ζ1 және спр2Ζ2 пайда болуына соқтырады.
Күштер мен моменттер теңдеулері былай жазылады:
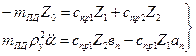 (14.6)
(14.6)
мұнда  - 0y осі (чертеж жазықтығына перпендикуляр) арқылы алынған рессорлы массаның инерциялық радиусі; Jy – сол ось арқылы алынған рессорлы массаның инерция моменті; а п, в п – рессорлы масса центрінен алдыңғы және артқы осьтерге дейінгі аралықтар.
- 0y осі (чертеж жазықтығына перпендикуляр) арқылы алынған рессорлы массаның инерциялық радиусі; Jy – сол ось арқылы алынған рессорлы массаның инерция моменті; а п, в п – рессорлы масса центрінен алдыңғы және артқы осьтерге дейінгі аралықтар.
Жоғарыдағы теңдеулерді шешкенде келесі коэффициенттерді аламыз:
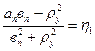 ;
; 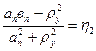 ;
;
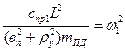 ;
; 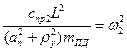 .
.
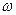 1 және
1 және 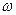 2 коэффиценттерін парциалдық (жеке) жиіліктер деп атайды, яғни күрделі тербелмелі жүйенің бір ғана еркіндік дәрежесі арқылы болатын тербеліс жиілігі, сонда басқа еркіндік дәрежелер арқылы ешқандай жылжулар болуы мүмкін емес.
2 коэффиценттерін парциалдық (жеке) жиіліктер деп атайды, яғни күрделі тербелмелі жүйенің бір ғана еркіндік дәрежесі арқылы болатын тербеліс жиілігі, сонда басқа еркіндік дәрежелер арқылы ешқандай жылжулар болуы мүмкін емес.
Егер В нүктесінің жылжуын болдырмасақ, онда А нүктесінің гармоникалық тербелісінің теңдеуі мына түрге келеді (14.4-сурет):
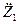 +
+ 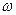 12Ζ1 =0. (14.7)
12Ζ1 =0. (14.7)
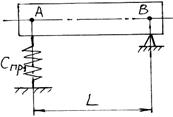
14.4-сурет – В нүктесінің жылжуы болмағанда тербелмелі жүйе.
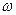 1 жиілігі осы еркіндік дәреже бойынша парциялдық жиілік болады.
1 жиілігі осы еркіндік дәреже бойынша парциялдық жиілік болады.
Егер А нүктесінің жылжуын болдырмасақ, онда В нүктесінің гармоникалық тербелісінің теңдеуі мына түрге келеді (14.5-сурет):
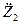 +
+ 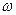 22Ζ2 =0. (14.8)
22Ζ2 =0. (14.8)
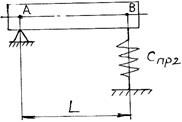
14.5-сурет – А нүктесінің жылжуы болмағанда тербелмелі жүйе.
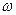 2 жиілігі осы еркіндік дәреже бойынша парциалдық жиілік болады.
2 жиілігі осы еркіндік дәреже бойынша парциалдық жиілік болады.
Рессорлы массаның тербелістерінің өзіндік жиіліктері тек ғана парциалдық жиіліктер мен байланыс коэффиценттеріне тәуелді екені байқалады.
Байланыс коэффиценттеріне (αп в п-ρ2y) айырмашылығы негізгі әсерін тигізеді. 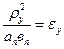 қатынасын рессорлы массалардың үлестірілу коэффиценті дейді. Егер εy=1 болса, онда αп в п=ρ2y және екі байланыс коэффиценті нольге тең болады. Бұл А және В нүктелерінің тербелістері тәуелсіз екенін көрсетеді, яғни рессорлы массаның тербелістерін зерттегенде оны өзара тәуелсіз екі бөліктен тұрады деп есептеуге болады, сонда бірінші бөлік mпд1 алдыңғы аспаға, ал екінші бөлік mпд2 артқы аспаға тіренеді. mпд1 және mпд2 массаларының тербелістерінің жиіліктері парциалдық жиіліктердің формулаларынан табылады. ρ2y =αп в п екенін ескеріп, табатынымыз:
қатынасын рессорлы массалардың үлестірілу коэффиценті дейді. Егер εy=1 болса, онда αп в п=ρ2y және екі байланыс коэффиценті нольге тең болады. Бұл А және В нүктелерінің тербелістері тәуелсіз екенін көрсетеді, яғни рессорлы массаның тербелістерін зерттегенде оны өзара тәуелсіз екі бөліктен тұрады деп есептеуге болады, сонда бірінші бөлік mпд1 алдыңғы аспаға, ал екінші бөлік mпд2 артқы аспаға тіренеді. mпд1 және mпд2 массаларының тербелістерінің жиіліктері парциалдық жиіліктердің формулаларынан табылады. ρ2y =αп в п екенін ескеріп, табатынымыз:
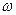 12 =
12 = 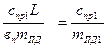 . (14.9)
. (14.9)
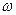 22 =
22 = 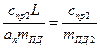 . (14.10)
. (14.10)
η1 және η2 кішілеу мәндерінде mпд1 массасының негізгі тербелістері 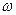 1 аз ғана айырмашылығы бар жиілікпен жүреді. Олардың үстіне түсетін
1 аз ғана айырмашылығы бар жиілікпен жүреді. Олардың үстіне түсетін 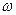 2 жақындау жиіліктегі тербелістің амплитудасы тіпті азғантай болады, сонда бұл тербелістің ықпалы тіпті байқалмайды. Осылай
2 жақындау жиіліктегі тербелістің амплитудасы тіпті азғантай болады, сонда бұл тербелістің ықпалы тіпті байқалмайды. Осылай 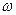 1 жақындау жиіліктегі тербелістің mпд2 массасының негізгі тербелістеріне тіпті ықпалын тигізбейді. Егер 0,8αп в п<ρ2y<1,2αп в п болса, тербелістердің өзіндік жиіліктерінің парциалдық жиіліктерден айырмашылығы 5-6% аспайды.
1 жақындау жиіліктегі тербелістің mпд2 массасының негізгі тербелістеріне тіпті ықпалын тигізбейді. Егер 0,8αп в п<ρ2y<1,2αп в п болса, тербелістердің өзіндік жиіліктерінің парциалдық жиіліктерден айырмашылығы 5-6% аспайды.
Бұл жағдайларда mпд1 және mпд2 массаларының тербелістерін шын мәнісінде тәуелсіз деп есептеуге болады. Толық жүктелген жеңіл және жүктік автомобильдерде қозғалыс кезінде 0,8αп в п<ρ2y<1,2αп в п шарты орындалады.
Дата добавления: 2015-09-04; просмотров: 105 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Автомобиль – тербелмелі жүйе | | | Сөну ескерілмегенде рессорлы және рессорсыз массалардың еркін тербелісі |