Бүйірлік кету ескерілгенде автомобиль бұрылуының кинематикасы

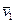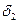Бүйірлік кету болған кезде алдыңғы және артқы осьтердің жылдамдық векторлары және бүйір бағытта қатты доңғалақтардың бағыттарымен салыстырғанда сәйкес және бүйірлік кету бұрыштарына ауады (9.8-сурет).

9.8-сурет – Бүйір бағытта созылғыш доңғалақтары бар автомобильдің бұрылу схемасы

Осы векторларға жүргізілген перпендикулярдың қиылысқан нүктесі автомобильдің бұрылу радиусты лездік бұрылу центрін береді .

Басқарылатын доңғалақтардың бұрылу бұрышы мен бұрылу және доңғалақтардың бүйірлік кету бұрыштарының және 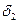арасындағы байланысты анықтаймыз.

.

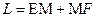және үшбұрыштарынан табатынымыз:

және .

Сонда

.

Осыдан:

. (9.18)

Автомобильдің үлкендеу жылдамдықтарында бұрышы аздау болады, онда осы бұрыштардың тангенстерін радианмен өлшенген осы бұрыштардың өздеріне алмастыруға болады:

. (9.19)

Бүйір бағытта қатты доңғалақтары бар автомобильдің кинематикалық радусына қарағанда бұрылу радиусі , бұрылу бұрышы -ға және доңғалақтардың бүйірлік кету бұрыштары және 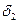-ге байланысты болады. Осыған сәйкес автомобильдің нормалық, аздау және артық бұрылғыштығы болады.

Нормалық, егер және .

Аздау, егер 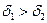және .

Артық, егер және .

Автомобильдің бұрылғыштық қасиетіне байланысты бірдей жағдайларда оның қозғалыс траекториясы әртүрлі болады.

Артық бұрылғыштығы бар автомобиль бұрылғыштығының жойылуы бүйірлік күш болмаған кезде басталуы мүмкін. Бұл жағдай автомобиль жылдамдығы аумалы шамаға жеткенде орын алуы мүмкін. Бұл жылдамдықты есептейтін формула табу үшін жоғарыда табылған байланысты былай өзгертеміз:

.

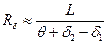Осыдан

. (9.20)

Тек қана центрден тепкіш күшті ескеріп, алдыңғы және артқы осьтерге әсер ететін жүктемелерді 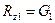және деп алып, табатынымыз:

; (9.21)

; (9.22)

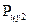мұнда және -алдыңғы және артқы доңғалақтарға түсетін центрден тепкіш күштің көлденең құрастырушылары; және -алдыңғы және артқы доңғалақтардың бүйірлік кетуге қарсылық коэффициенттері.

Жылдамдық үлкейген сайын бүйірлік кету бұрыштарының айырмашылығы әрдайым үлкейіп отырады және радиусты траекториямен автомобиль қозғалуы үшін басқарылатын доңғалақтардың бұрылу бұрышы сәйкес азайып отыруы керек.

Автомобиль жылдамдығы аумалы шамасына жеткенде оның радиусты траекториямен қозғалу үшін бұрышы нольге тең болуы керек.

Сонда немесе

. (9.23)

Осы теңдеуді өзгертіп, табатынымыз:

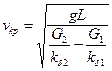. (9.24)

Бұл формулаға автомобильдің бұрылу радиусі кірмейді, бұлай болса автомобиль жылдамдығы аумалы шамаға жеткенде оның тіке қозғалуға тіпті мүмкіншілігі болмайды.

Нормалық бұрылғыштықты автомобиль үшін:

, сондықтан .

Аздау бұрылғыштықты автомобильдер үшін:

, аумалы жылдамдығы болмайды (жорамалдық шама).

Сондықтан автомобиль жобалағанда оның аздау бұрылғыштық қасиетін алады. Бұл үшін автомобильдің ауырлық центрін алдыңғы оське жақындатып алады , алдыңғы доңғалақтың шиналарының ішіндегі ауа қысымын азайтады.

Қосарланған артқы доңғалақтары бар жүктік автомобильдердің болғанымен алдыңғы доңғалақтардың бүйірлік кету бұрыштары артқы доңғалақтардікімен салыстырғанда үлкен болады. Бұл аздау бұрылғыштықты қамтамасыз етеді.

Артық бұрылғыштықты автомобильдің аумалы жылдамдық шамасы автомобильдің тарту-жылдамдық қасиеттерінен табылатын ең үлкен жылдамдығынан едәуір үлкен болуы керек:

.

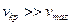Негізгі әдебиет: 4.1нег.133-158б.

Қосымша әдебиет: 4.4қос.87-104б.

Дата добавления: 2015-09-04