Структурный анализ механизма

Механизм – искусственно созданная система тел, предназначенная для передачи и преобразования движения одного или нескольких твёрдых тел в требуемое движение других твёрдых тел.

Кривошип – звено, совершающее полнооборотное вращение вокруг неподвижной оси.

Коромысло – звено, совершающее качательное движение относительно неподвижной оси.

Шатун – звено, которое образует кинематические пары только с подвижными звеньями.

Ползун – звено, совершающее возвратно-поступательное движение.

Стойка (направляющая) – неподвижное звено.

Основные задачи структурного анализа механизма включают в себя:

1) определение количества звеньев, кинематических пар и их класса;

2) определение количества степеней свободы механизма в зависимости от числа подвижных звеньев, числа и класса кинематических пар;

3) разделение механизма на структурные группы и определение их класса.

Схема рычажного механизма глубинного насоса приведена на рисунке 3.

Рисунок 1 – Кинематическая схема

Рисунок 3 – Кинематическая схема рычажного механизма

Число степеней свободы кинематической цепи W относительно одного из ее звеньев называют степенью ее подвижности. Для определения степени подвижности любой кинематической цепи необходимо подсчитать число степеней свободы всех подвижных звеньев (n), полагая их не связанными между собой. Затем из этого числа следует вычесть число связей, наложенных на звенья кинематическими парами. Кинематические пары 4-го (р₄) и 5-го (р₅) классов накладывают соответственно одну и две связи.

Структурная формула Чебышева для определения числа степеней свободы плоского механизма имеет вид

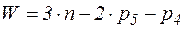, (2.1)

где n – число подвижных звеньев;

p₅ и p₄ – число кинематических пар 5 и 4 классов соответственно.

При анализе структуры механизма рекомендуется:

а) определить W механизма и выбрать начальное звено;

б) отсоединить структурные группы нулевой подвижности, начиная с групп, наиболее отдаленных от начальных звеньев;

в) следить за тем, чтобы степень подвижности кинематической цепи механизма до и после отделения структурной группы осталась неизменной;

г) помнить о том, что каждая кинематическая пара и каждое звено могут входить только в одну структурную группу или в один начальный механизм.

Структурная группа или группа Ассура – кинематическая цепь, получающая нулевую подвижность после присоединения ее к стойке.

Для групп, содержащих пары только 5-го класса, имеем

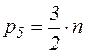. (2.2)

Анализ структуры рычажного механизма показал, что механизм шестизвенный, подвижных звеньев 5, кинематические пары 4 класса p₄ отсутствуют, кинематических пар 5 класса p₅ =7. Кинематические пары O, A, B, C, D, E’ - вращательные (ВКП), кинематическая пара Е – поступательная (ПКП).

Для заданного рычажного механизма число степеней свободы механизма определяем по формуле Чебышева:

= .

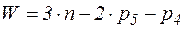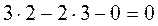Так как W = 1, то механизм имеет одно ведущее звено. Ведущим звеном является кривошип ОА.

Отсоединяем от механизма структурные группы Ассура начиная с самой удаленной от начального звена и определяем их число степеней свободы.

Для диады №1 (звенья 4 и 5) число степеней свободы определяем по формуле (2.1):

= .

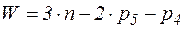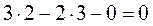При этом число степеней свободы оставшегося механизма не изменилось.

= .

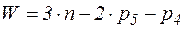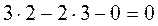Для диады №2 (звенья 2 и 3) число степеней свободы определяем по формуле (2.1):

= .

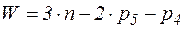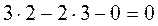Число степеней свободы группы начальных звеньев (ГНЗ) определяем по формуле (2.1):

= .

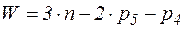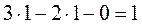Степень подвижности начального механизма 1-го класса (звенья 1 и 6) осталась неизменной.

Поскольку класс механизма соответствует наивысшему классу группы, входящей в его состав, то заданный рычажный механизм будет относиться к механизмам 2-го класса [1].

Рисунок 4 – Структурные группы рычажного механизма

Дата добавления: 2015-09-01