Уравнивание триангуляции коррелатным способом.

Уравнивание коррелатным способом выполняют по углам или – более строго – по направлениям. Условные уравнения разделяют на угловые и синусные. Угловыми называют линейные условия, имеющие коэффициенты ±1 и 0. Синусными называют нелинейные условные уравнения, в которых содержатся синусы. В триангуляции после устранения невязок угловых условий дирекционный угол любой стороны сети определяется однозначно независимо от пути его передачи от исходных дирекционных углов.

В триангуляции имеются следующие виды угловых условий.

Условия фигур возникают в треугольниках и многоугольниках. В плоском треугольнике (рис.1а),

1 + 2 + 3 – 180⁰ = ω

где 1, 2, 3 – измеренные значения углов треугольника; ω – невязка в треугольнике. При уравнивании к углам J определяют поправки (J) и получают

1+ (1) + 2 + (2) + 3 + (3) – 180⁰ = 0.

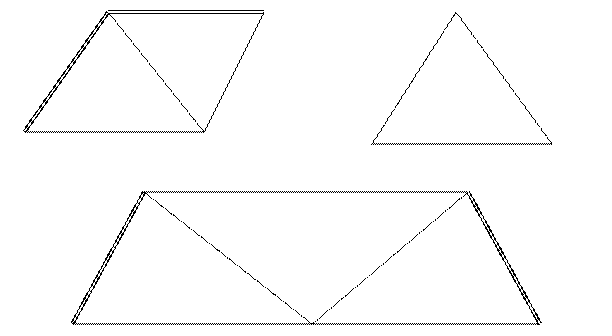
Рис.1

Из сравнения этих выражений находят условие фигур

(1) + (2) + (3) + ω = 0.

При уравнивании направлений для треугольника условное уравнение фигур имеет вид (рис1.б)

-(1) + (2) – (3) + (4) – (5) + (6) + ω = 0,

где ω = [2-1] + {4-3] + [6-5] – 180⁰.

Условия горизонта возникают на пунктах, на которых в уравнивание включены все углы, образуемые смежными направлениями, сумма этих углов равна 360⁰, т.е.

(1) + (2) + …+(N) + ω = 0.

При уравнивании по направлениям условий горизонта не возникает.

Условия исходных дирекционных углов возникают при вставке цепочки треугольников в угол или между исходными сторонами и состоят в том, что сумма уравненных углов должна равняться величине жесткого угла или дирекционный угол стороны СД (рис.1.в) должен равняться его вычисленному значению от исходного дирекционного угла стороны АВ с использованием уравненных значений углов треугольников.

На рис.1.а α_ВС + 6 + 3 – α_ВА = ω.

После введения поправок и преобразований получаем условное уравнение

(3) + (6) + ω = 0.

Для сети на рис.1.в.

α_АВ ± 180⁰ – С₁ ± 180⁰ + С₂ ± 180⁰ – С₃ – α_СД = ω. (1)

После введения поправок и преобразований находим условное уравнение

– (С₁) + (С₂) – (С₃) + ω = 0.

Если дирекционные углы α_АВ и α_СД (рис.1.в) получены из измерений и поправки (α_АВ) и (α_СД) в их значениях определяют из уравнивания сети, то условное уравнение дирекционных углов в этом случае имеет вид

– (С₁) + (С₂) – (С₃) + (α_АВ) - (α_СД) + ω = 0,

где ω определяют по формуле (1).

Синусные условия состоят из полюсных, базисных и координатных; их учет необходим для однозначного определения длины любой стороны сети независимо от пути ее определения от исходных сторон. Координатные условия обеспечивают однозначное получение координат любого пункта сети.

Полюсные условия возникают в центральных системах и геодезических четырехугольниках, так как в этих фигурах одна сторона является избыточной. На рис.2 с учетом замены отношения сторон отношением синусов противолежащих им углов имеем

Дата добавления: 2015-09-02