Двухгрупповой метод

При уравнивании больших сетей триангуляции возникает много условных и нормальных уравнений, что приводит к трудоемким вычислениям. Для уменьшения объема вычислений Крюгер предложил двухгрупповой метод, в котором условные уравнения делят на две группы, решают уравнения первой группы, находят первичные поправки v’. Затем преобразуют уравнения второй группы и в результате их решения получают поправки v” и окончательные поправки v = v’+v”, такие же, что и при совместном решении уравнений.

Н.А. Урмаев предложил включать в первую группу все условные уравнения фигур неперекрывающихся треугольников. При этом нормальные уравнения первой группы принимают вид

,

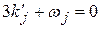а вычисление поправок 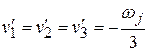сводится к распределению невязок треугольников с обратным знаком поровну на три угла.

По исправленным первичным поправками углам в каждом треугольнике вычисляют свободные члены условных уравнений второй группы и преобразованные коэффициенты

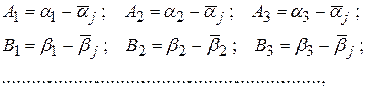
где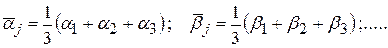

Контроль: [A] = [B] = … = 0.

Решив нормальные уравнения второй группы, находят коррелаты, позволяющие вычислить вторичные поправки v”, которые вводят в предварительно уравненные углы.

Дата добавления: 2015-09-02