Індекс Шеннона.

Мак-Артур (1955) і Маргалеф (1957) вперше застосували для оцінки в дослідженні видової стійкості та різноманітності угруповання теорію інформації. Теорія інформації ґрунтується на вивченні ймовірності настання ланцюга подій. Результат виражається в одиницях невизначеності або інформації. Шеннон в 1949 р. вивів функцію, яка стала називатися індексом різноманітності Шеннона.

Розрахунки індексу різноманітності Шеннона припускають, що особини потрапляють у вибірку випадково з "невизначено великої" (тобто практично нескінченної) генеральної сукупності, причому у вибірці представлені всі види генеральної сукупності. Невизначеність буде максимальною, коли всі події (N) будуть мати однакову ймовірність настання (р_i, = 1 / N). Вона зменшується в міру того, як, частота деяких подій зростає в порівнянні з іншими, аж до досягнення мінімального значення (нуля), коли залишається одна подія і є впевненість в його наступі.

Індекс Шеннона розраховується за формулою:

де величина р_i, - доля особин i -го виду.

У вибірці істинне значення р_i, невідомо, але оцінюється як п_i,/N.

Причини помилок в оцінці різноманітності з використанням цього індексу полягають, насамперед, у тому, що неможливо включити у вибірку всі види реального угруповання.

При розрахунку індексу Шеннона часто використовується двійковий логарифм, але прийнятно також використовувати й інші підстави логарифма (десятковий, натуральний).

Індекс Шеннона звичайно варіює в межах від 1,5 до 3,5, дуже рідко перевищуючи 4,5.

Дисперсію індексу Шеннона розраховують за формулою:

Якщо значення індексу Шеннона розрахувати для декількох вибірок, то отримане розподіл величин підпорядковується нормальному закону. Ця властивість дає можливість застосовувати потужну параметричну статистику, включаючи дисперсійний аналіз. Застосування порівняльного параметричного і дисперсійного аналізу корисно при оцінці різноманітності різних місцеперебувань, коли є повторності.

Для перевірки значущих відмінностей між вибірковими сукупностями значень індексу Шеннона Хатчесон запропонував використовувати параметричний критерій Стьюдента:

Число ступенів свободи визначаються за допомогою рівняння:

де N₁; и N₂- загальне число видів в двох вибірках.

На основі індексу Шеннона можна обчислити показник вирівненності Е (відношення спостережуваного різноманіття до максимального):

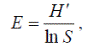Е ϵ [0; I], причому Е = 1 при рівному достатку всіх видів.

Індекс Шеннона виявився найпопулярнішим в оцінці даних за різноманітністю і застосовується частіше за інших.

Індекс Бриллуену.

Не завжди дослідники здатні гарантувати випадковий відбір об'єктів у вибіркову сукупність або врахувати всі види угруповання. Це відбувається зазвичай через недосконалі методів вилову тварин. Не можна забезпечити випадковість потрапляння об'єктів у вибірку при вилові комах на світло (залучаються види, активні тільки вночі, і випадають зі списку видів форми з денною активністю). Дуже різняться списки видів павукоподібних, принесених в гнізда великий синицею і зібраних в біотопі традиційними методами, рекомендованими при зборі безхребетних. Придатною формою інформаційного індексу в таких випадках може бути індекс Бріллуена, що визначається за формулою:

Індекс Бріллуена дає схожу з індексом Шеннона величину різноманітності, ред ко перевищуючи 4,5. Однак при оцінці одного і того ж масиву даних його величина нижче індексу Шеннона. Це пояснюється тим, що в ньому немає невизначеності, властивої індексу Шеннона.

Выравненність визначаються за формулою:

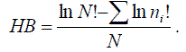где [N/8] - ціла частина відношення N/S, а r = N-S * [N/S].

Цим індексом мало користуються, так як він важко обчислюється і якщо вибірка мала - призводить до невірних висновків. Однак цей індекс рекомендується використовувати, якщо оцінюється колекція, а не випадкова вибірка, й якщо відомий повний склад угруповання.

Заходи домінування приділяють основну увагу достатку самих звичайних видів, а не видовому багатству. Кращим серед індексів домінування вважається індекс Сімпсона. Його іноді називають індексом Юла, оскільки він нагадує міру, розроблену Юлом для оцінки словникового запасу.

Індекс Сімпсона описує вірогідність приналежності будь-яких двох особин, випадково відібраних з невизначено великої угруповання до різних видів, формулою:

где р _i -доля особин i -го виду.

Для розрахунку індексу використовується формула, відповідна кінцевому угруповання:

где n_i- число особин i -го виду, а N- загальне число особин.

У міру збільшення В різноманітність зменшується. Тому індекс Сімпсона час то використовують у формі (1 - В). Ця величина зветься "ймовірність міжвидових зустрічей" і варіює і межах від 0 до 1. Він дуже чутливий до присутності у вибірці найбільш рясних видів, але слабо залежить від видового багатства. Висока або низька величина індексу визначається типом розподілу видових достатку для випадків, коли число видів перевищує 10. Багато авторів вважають, що найкраща міра домінування - це "індекс полідомінантності":

де i = 1,2,3,...S; S1 c [1;∞]

Дата добавления: 2015-09-02