Контроль по запрещенным комбинациям.

В вычислительных машинах и устройствах используются специальные схемы, обнаруживающие появление запрещенных комбинаций, например обращение по несуществующему адресу, обращение к несуществующему устройству, неправильный выбор адреса.

Корректирующие коды. Код Хэмминга строится таким образом, что к имеющимся m информационным разрядам слова добавляется определенное число k контрольных разрядов, которые формируются перед передачей информации путем подсчета четности суммы единиц для определенных групп информационных разрядов. Контрольное устройство на приемном конце образует из принятых информационных и контрольных разрядов путем аналогичных подсчетов четности адрес ошибки. Ошибочный разряд корректируется автоматически. Код с d = 3 исправляет одну ошибку, с d = 4 обнаруживает двойные и исправляет одиночные ошибки. Число разрядов удовлетворяет соотношению

k>= Iog₂(n+ 1).

Чтобы число в регистре ошибок указывало номер позиции ошибочного знака, группы для каждой проверки выбираются по следующему правилу.

Первая проверка, в результате которой получается 0 или 1 в первом (младшем) разряде регистра, охватывает все нечетные позиции кода, включая и позицию принадлежащего этой группе контрольного знака. Эта операция записывается таким образом:

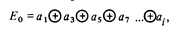где а1, а₃,..., аi — двоичные символы, размещенные в разрядах с порядковыми номерами 1,3, и т д.

Вторая проверка охватывает все позиции, номер которых в двоичном исчислении 1 во втором разряде (т.е. 2, 3,6, 7... и т.д.),т.е.

Аналогичным образом определяются другие проверки

Образующее число Е₀Е₁... Е^ считается корректирующим.

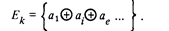Для ОЗУ емкостью свыше 512К байт выпускаются специализированные БИС, в которых реализуется схема контроля на основе Хэмминга, так как этот код не требует сложных кодирующих и декодирующих устройств и требует незначительных затрат времени на формирование дополнительных проверочных соотношений и синдрома. Выбор этого кода обусловлен тем, что физико-технологические испытания и статистика подтверждают наличие в ОЗУ ошибок малой кратности. Кроме того, код позволяет унифицировать принципиальную схему кодирующих и декодирующих устройств по числу входов и нагрузок логических элементов, уменьшить сложность устройств обнаружения многократных ошибок, обеспечить увеличение формата информационных данных путем использования нескольких БИС, сохранив при этом минимальный коэффициент избыточности, допускает программную обработку синдромов ошибок.

Циклические коды применяют в системах с последовательной передачей двоичных символов, составляющих слово. Типичным примером таких систем служит канал связи, по которому осуществляется передача дискретных данных. Такая передача применяется при записи и чтении информации в некоторых типах внешних накопителей на магнитных лентах и дисках.

Особенность циклических кодов, определяющая их название, состоит в том, что если n-значная кодовая комбинация а₀a₁ a₂... а_п-1 принадлежит данному коду, то и комбинация а_n-1a₀ a₁ a₂... а_п-2 полученная циклической перестановкой знаков, также принадлежит этому коду.

Основным элементом кодирующей и декодирующей аппаратуры при работе с такими кодами служит сдвигающий регистр с обратной связью, обладающий необходимыми циклическими свойствами.

Двоично кодированное n-разрядное число представляется полиномом (n -- 1)-й степени некоторой переменной х, причем коэффициентами полинома являются двоичные знаки соответствующих разрядов. Запись и чтение чисел, так же как и их последовательная передача, производится, начиная со старшего разряда. Поэтому при описании циклических кодов записывают числа и соответствующие им полиномы так, чтобы старший разряд оказывался справа. Например, число 101101 представляется полиномом 6-й степени

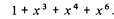
Упомянутая выше циклическая перестановка соответствует умножению полинома на х, при котором х**n заменяется на 1 и переходит в начало полинома. В нашем примере такая операция дает 1 + х + х**4 + х**5. Такие полиномы рассматриваются в соответствии с законами обычной алгебры с той лишь разницей, что сложение осуществляется по модулю 2 (поразрядное сложение без переносов).

Циклический код n-значного числа, как и всякий систематический код, состоит из т информационных знаков и k контрольных, причем последние всегда занимают k младших разрядов. Так как последовательная передача производится, начиная со старшего разряда, контрольные знаки передаются в конце кода.

Код образуется с помощью так называемого порождающего полинома Q(x) степени k и именно видом этого полинома определяются все свойства кода — избыточность и корректирующая способность.

Кодовым полиномом F(x) является полином степени, меньшей т + k, если он делится без остатка на порождающий полином Q(x) степени k. После передачи числа или после чтения его с магнитной ленты декодирование состоит в выполнении процедуры, соответствующей делению полинома Н(х), который представляет принятое число, на Q(x). При отсутствии ошибок Н(х) = F(x) и деление будет выполнено без остатка. Наличие ненулевого остатка указывает на то, что при передаче или хранении произошли ошибки.

Принципиально наиболее простым способом кодирования кажется умножение полинома Р(х), представляющего информационные символы, на Q(x). Но в этом случае код не будет систематическим, так как контрольные знаки не будут выделены. Поэтому применяется следующая процедура. Информационный полином Р(х) степени, меньшей т, который необходимо закодировать, умножается на х**k, что соответствует сдвигу слова на k разрядов вправо (в сторону старших разрядов). Полученный таким образом полином (x**k)*P(x) делится на Q(x) для определения остатка R(x). Остаток R(x) складывается с x^kP(x) и, таким образом,

Практически применяемая процедура кодирования еще более проста. Так как интересуются только остатком, а частное в конечном результате не используют, то можно производить лишь последовательное вычитание по модулю 2 из делимого и получающихся разностей до тех пор, пока разность не будет иметь более низкую степень, чем делитель. Эта разность и есть остаток. Такой алгоритм реализуется с помощью k-разрядного сдвигающего регистра, имеющего обратные связи, соответствующие виду порождающего полинома Q(x). Таким образом, проблема разработки циклического кода для обнаружения заданных типов ошибок сводится к нахождению нужного порождающего полинома Q (х).

Дата добавления: 2015-09-02