Политропные процессы

До сих пор рассматривались процессы, у которых имелись вполне определенные признаки: изохорный процесс осуществлял­ся при постоянном объеме; изобарный — при постоянном давле­нии; изотермический — при постоянной температуре; адиабат­ный— при отсутствии теплообмена между рабочим телом и внеш­ней средой. Наряду с этими процессами можно представить еще бесконечное множество процессов, у которых имеются другие постоянные признаки.

Условились всякий процесс идеального газа, в котором удель­ная теплоемкость является постоянной величиной, называть политропным процессом, а линию процесса — политропой. Из определения политропного процесса следует, что основные термодинамические процессы — изохорный, изобарный, изотерми­ческий и адиабатный,— если они протекают при постоянной удель­ной теплоемкости, являются частными случаями политропного процесса. Если теплоемкость зависит от температуры, то нужно найти среднюю теплоемкость, чтобы процесс стал политропным.

ПОКАЗАТЕЛЬ ПОЛИТРОПЫ

Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:

где р — давление, V — объем газа, n — «показатель политропы».

. Здесь — теплоёмкость газа в данном процессе, и — теплоемкости того же газа, соответственно, при постоянном давлении и объеме.

В зависимости от вида процесса, можно определить значение n:

• Изотермический процесс: , так как , значит, по закону Бойля — Мариотта 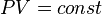, и уравнение политропы вынуждено выглядеть так: .

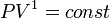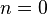• Изобарный процесс: , так как 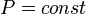, и уравнение политропы вынуждено выглядеть так: .

• Адиабатный процесс: (здесь 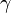— показатель адиабаты), это следует из уравнения Пуассона.

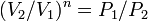• Изохорный процесс: , так как , и в процессе , а из уравнения политропы следует, что , то есть, что , то есть , а это возможно, только если является бесконечным.

Теория подобия – это наука о подобных явлениях. Подобными явлениями называются такие физические явления, которые одинаковы качественно по форме и по содержанию, т.е. имеют одну физическую природу, развиваются под действием одинаковых сил и описываются одинаковыми по форме дифференциальными уравнениями и краевыми условиями. Обязательным условием подобия физических явлений должно быть геометрическое подобие систем, где эти явления протекают. Два физических явления будут подобны лишь в том случае, если будут подобны все величины, которые характеризуют их. Для всех подобных систем существуют безразмерные комплексы величин, которые называются критериями подобия.

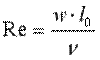— критерий Рейнольдса, характеризующий режим движения жидкости;

— критерий Грасгофа, характеризующий подъемную силу, возникшую вследствие разности плотности жидкости. Здесь β - коэффициент объёмного расширения жидкости;

— критерий Прандтля, определяющий физические свойства жидкости.

Критерии, составленные из величин, определяющих характер процесса, но не включающие искомых величин, называются определяющими, а критерии, включающие искомые величины, - неопределяющими. Так, при расчёте конвективного теплообмена критерий Nu не является определяющим, так как в него входит искомая величина α. Критерии же Re и Pr в этих же расчётах – определяющие.

Дата добавления: 2015-09-02