Нелинейными членами разложения (остатком R) пренебрегают.
Решение приводит к образованию системы нормальных уравнений коррелат | Подлежит оценке точности весовая функция | Решение нормальных уравнений по алгоритму Гаусса | Для оценки точности результатов измерений вычисляют | Блок-схема коррелатного способа уравнивания | Уравнивание нивелирной сети коррелатным способом | Составим условные уравнения связи. | Следует иметь в виду, что количество запасных знаков, оставляемых при решении нормальных уравнений, зависит от точности невязок w и соответствует представленному в данном примере. | Уравнивание геодезического четырехугольника коррелатным способом | Составим условные уравнения связи. |
Обозначают:
Фj(y1, y2,..., yn) = wj
- невязки - свободные члены условных уравнений поправок;

- коэффициенты условных уравнений поправок - частные производные от функций Фj, вычисляемые по результатам измерений.
 (6)
(6)
- система условных уравнений поправок или в матричном виде:
АrnVn1 + Wr1 = 0. (7)
Здесь  - матрица коэффициентов;
- матрица коэффициентов;
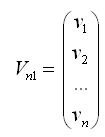 - вектор поправок к результатам измерений;
- вектор поправок к результатам измерений;
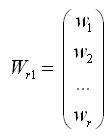 - вектор невязок.
- вектор невязок.
Дата добавления: 2015-09-01; просмотров: 69 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.011 сек.)


 (6)
(6) - матрица коэффициентов;
- матрица коэффициентов;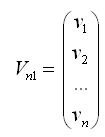 - вектор поправок к результатам измерений;
- вектор поправок к результатам измерений;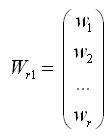 - вектор невязок.
- вектор невязок.