Под условием МНК

Коррелатный способ уравнивания

Условные уравнения

Пусть измерено n величин у₁, у₂,..., у_n с весами р₁, р₂,..., р_n.

Обозначим t - число необходимых измерений;

r = n - t (1)

- число избыточных измерений.

Истинные значения измеренных величин Y_i связаны между собой уравнениями:

Ф_j(Y₁, Y₂,..., Y_n) = 0, (j = 1, 2,..., r). (2)

Уравнения, выражающие математическую связь между истинными значениями измеренных величин, называются условными уравнениями связи. В систему включают только независимые уравнения в количестве r = n - t, (r < n). Если число уравнений будет больше r, появятся зависимые уравнения и задача уравнивания станет неопределенной. Если число уравнений окажется меньше r, после уравнивания останутся невязки.

Подстановка в уравнения (2) результатов измерений приводит к системе:

Ф_j(y₁, y₂,..., y_n) = w_j, (j = 1, 2,..., r), (3)

в которой невязки w_j являются истинными ошибками соответствующих функций Ф_j.

Для устранения невязок отыскивают поправки v_i к результатам измерений из решения системы

Ф_j(y₁ + ν₁, y₂ + ν₂,..., y_n + ν_n) = 0, (j = 1, 2,..., r) (4)

под условием МНК

[pv²] = min. (5)

Условные уравнения (4) могут иметь нелинейный вид. Способов решения систем нелинейных уравнений произвольного вида не существует. Чтобы решить задачу, функции (4) приводят к линейному виду разложением в ряд Тейлора. Полагая, что ν_i << y_i, рассматривают поправки ν_i, как приращения аргументов y_i. Функции Ф_j должны быть дифференцируемы.

Ф_j(y₁ + ν₁, y₂ + ν₂,..., y_n + ν_n) = Ф_j(y₁, y₂,..., y_n) +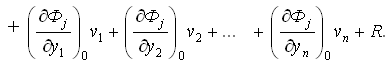

Дата добавления: 2015-09-01