Движении

Для этого следует воспользоваться формулами раздела “ Кинематика точки” ¾ при траекторном (естественном) способе задания ее движения.

· Траекторная координата точки М, заданная уравнением

= + A О sin k t,

после подстановки – =0 м; A О = R /2 см,, k= , примет вид = R /2· sin (π/6) ·t. (4.1)

При t=1с: = R /2·sin (π/6) 1= R /2· 1/2 = R /4 м.

_окр =2 R м; ( ) / ( _окр) = (R /4) / (2 R) =1/8

a =(1/8) ( _окр=360°) = 45°;

На рис.4.2 определено положение точки М на диске в момент времени 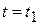(а не в произвольном положении, показанном на рис.4.1) в подвижной (относительной) системе отсчета ¾ при естественном (траекторном) способе задания ее движения, при котором >O.

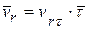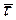· Cкорость точки М: , где ─ касательная к траектории в данной точке, направленная всегда в сторону возрастания траекторной координаты s;

= (4.2)

= 6 π² 0,866 = 59,2 × 0,866 = 52,3 м/с; так как > 0, то ­­ .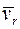

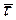·Ускорение точки М: 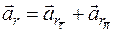, (4.3)

где ─ касательное, а ─ нормальное ускорения точки;

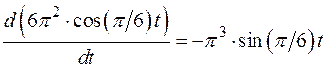= ; (4.4)

= - p³ 0,5= - 15,5 м/с2. Так как < 0, то ¯­ .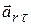

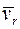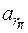
= ; = 51,3²/ 72 = 36,5 м/с2, (4.5)

где ρ ─ радиус кривизны траектории в данной точке.

Все векторы 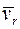, и определены для момента времени 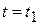и изображены на рис.4.2 (без определения ).

Дата добавления: 2015-09-05