Величина. называется плотностью убытков из-за неудовлетворительного спроса и играет важную

(24)

называется плотностью убытков из-за неудовлетворительного спроса и играет важную роль в управлении запасами. Заметим, что 0 £ r £ 1. Если значение с ₃ мало по сравнению с с _2, то величина r близка к нулю: когда с ₃ значительно превосходит с ₂, то r близка к 1. Недопустимость дефицита равносильна предположению, что с ₃ ® ¥ или r = 1.

Используя (24) основные формулы (22) и (23) можно записать компактнее:

, (25)

(26)

Следует учесть, что в силу (17) и (26) и 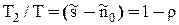. Поэтому утверждение о том, что плотность убытков из-за неудовлетворительного спроса равна r, означает, что в течение (1–r)100% времени от полного периода Т запас продукта будет отсутствовать.

Из сравнения (25) и (10) следует, что оптимальные объёмы партий для задач с дефицитом и без дефицита при одинаковых параметрах связаны соотношением:

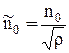(27)

откуда вытекает, что оптимальный объём партии в задаче с дефицитом всегда больше (в1/ Ör), чем для задач без дефицита.

Задача 4. Найти наиболее экономичный объём партии и интервал между поставками, сохраняя условия задачи 2, кроме недопустимости дефицита, если известно, что отсутствие на сборке каждой детали приносит в сутки убытки в размере 3,5 ден. ед.

Решение. По условию с₃=3,5. Ранее при решении задачи 2 было получено по формуле (9) =4335 и по (15) Т₀=13,2. Найдём плотность убытков из-за неудовлетворённого спроса по формуле (24): r=3,5/(0,35+3,5)=0,909, т.е. 100(1– 0,909)=9,1% времени между поставками детали на сборке будут отсутствовать.

Теперь оптимальный размер партии по формуле (27) . В силу (15) пропорционально увеличению 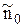должен увеличиться интервал между поставками, т.е.

.

Дата добавления: 2015-09-05