Статистическая детерминированная модель с дефицитом

В рассматриваемой модели будем полагать наличие дефицита. Это означает, что при отсутствии запасаемого продукта, т.е. при J(t)=0 спрос сохраняется с той же интенсивностью r(t)=b, но потребление запаса отсутствует – b(t)=0, вследствие чего накапливается дефицит со скоростью b. График изменения уровня запаса в этом случае представлен на рис. 3. Убывание графика ниже оси абсцисс в область отрицательных значений в отличие от графика на рис. 2 характеризует накопление дефицита.

Из рис. 4 видно, что каждый период «пилы» 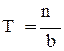разбивается на два временных интервала, т.е. T=T₁+T₂, где T₁ – время в течение которого производится потребление запаса, Т₂ – время, когда запас отсутствует и накапливается дефицит, который будет перекрыт в момент поступления следующей партии.

Рис. 4.

Необходимость покрытия дефицита приводит к тому, что максимальный уровень запаса s в момент поступления каждой партии теперь не равен её объёму n, а меньше его на величину дефицита n-s, накопившегося за время Т₂ (см. рис. 4).

Из геометрических соображения легко установить, что

(17)

В данной модели в функцию суммарных затрат С наряду с затратами С₁ (на пополнение запаса) и С₂ (на хранение запаса) необходимо ввести затраты С₃ – на штраф из-за дефицита, т.е.

С=С₁+С₂+С₃

Затраты С₁, как и ранее находим по формуле (11). В разд. 2.2 было показано, что затраты С₂ при линей ном расходе запаса равны затратам на хранение среднего запаса, который за время потребления Т₁ равен sT₁/2; поэтому с учётом (7) и (5) эти затраты составят

(18)

При расчёте затрат С₃ будем считать, что штраф за дефицит составляет в единицу времени с₃ на каждую единицу продукта. Так как средний уровень дефицита за период Т₂ равен (n-s), то штраф за этот период Т₂ составит , а за весь период q с учётом (7) и (19) –

(19)

Теперь учитывая (12), (18) и (19) суммарные затраты равны

(20)

Нетрудно заметить, что при n=s формула (19) совпадает с ранее полученной (8) в модели без дефицита.

Рассматриваемая задача управления запасами сводится к отысканию такого объёма партии и максимального уровня запаса, при которых функция С (19) принимает минимальное значение. Другими словами, необходимо исследовать функцию двух переменных С(n,s) на экстремум. Приравнивая частные производные к нулю, получим после преобразования систему уравнений:

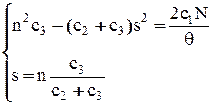(21)

Решая систему, получаем формулы наиболее экономичного объёма партии и максимального уровня запаса для модели с дефицитом[1]:

, (22)

. (23)

Дата добавления: 2015-09-05