
Читайте также:
|
Для проведения численных расчетов и процесса решения с помощью комплексных амплитуд необходимо заменить каждую переменную из формулы (18) формой комплексного числа. Тогда формула (18) примет вид:

 . (19)
. (19)
Найдем все переменные в комплексной форме. Согласно (4) для 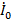 получим
получим
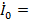 a + bj, (20)
a + bj, (20)
где a = 3 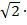 cos(-60
cos(-60  ) – действительная часть;
) – действительная часть;
b = 3  sin(-60
sin(-60  ) – мнимая часть.
) – мнимая часть.
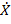 l определяется равенством
l определяется равенством
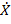 l = j ω L. (21)
l = j ω L. (21)
Далее,
 1 = R1 + 0
1 = R1 + 0  j = R1, (22)
j = R1, (22)
 2 = R2 + 0
2 = R2 + 0  j = R2, (23)
j = R2, (23)
 об =
об =  . (24)
. (24)
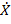 c определяется равенством
c определяется равенством
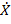 c =
c =  = - j
= - j  . (25)
. (25)
Комплексный вид сопротивления  примет вид
примет вид
 =
=  =
=  =
=  . (26)
. (26)
Тогда
 об = - j
об = - j  +
+  . (27)
. (27)
Введем обозначения
m = 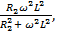 (28)
(28)
где m – это действительная часть комплексного сопротивления  об,
об,
k =  , (29)
, (29)
где k – это мнимая часть комплексного сопротивления  об.
об.
Запишем формулу для искомого тока  с учетом новых обозначений.
с учетом новых обозначений.

 =
=  =
=  (30)
(30)
Введем еще несколько обозначений для упрощения вида формулы (30):
α =  ; (31)
; (31)
β = 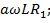 (32)
(32)
γ =  (33)
(33)
δ =  (34)
(34)
Окончательно для тока  имеем
имеем
 =
=  =
=  =
=  =
=  +
+  j. (35)
j. (35)
Отсюда получим амплитуду IR2m и начальную фазу φR2 для искомого тока.
IR2m = |  | =
| = 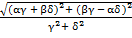 , (36)
, (36)
φR2 = arg ( ) = arctg
) = arctg  . (37)
. (37)
Далее, была составлена программа на языке высокого уровня C#. Программа производит расчеты на основе формул (36), (37), (31) – (34), (28), (29). На рисунке 3 приведено окно рабочей программы. В левой нижней части окна выставлены все исходные данные, в правой нижней части выводятся результаты, начальная фаза и амплитуда. В приложении А приведен исполняемый код кнопки “Расчет”. Так же дополнительно реализована в программе возможность расчета мгновенного значения тока на сопротивлении R2. По введенному пользователем времени (задается в секундах) в окне “ i(R2)(мгнов.) ” по нажатии кнопки “Мгнов.i” выдается ответ в амперах (либо в мА). Исполняемый код кнопки “Мгнов. i” приведен в приложении Б.

Рисунок 3 – Окно рабочей программы
С учетом заданных условий получились следующие значения:
- IR2m = 1,29 А;
- φR2 = -8,32  ;
;
- iR2 (0) = -3,3 мА.
Здесь iR2 (0) – это мгновенное значение тока на сопротивлении R2 в момент времени t = 0 сек.
Дата добавления: 2015-09-05; просмотров: 68 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Аналитический расчет токов | | | Проверка решения |