Аналитический расчет токов

В цепи, приведенной на рисунке 1 необходимо найти ток i_R2. Для этого достаточно найти амплитуду тока и начальную фазу, т.к. в данной цепи все воздействия гармонические и мгновенное значение тока можно просчитать, как

i _мгнов. = I_m sin(ωt + φ) (1)

где I_m – амплитудное значение тока;

φ – начальная фаза;

ω – циклическая частота генератора.

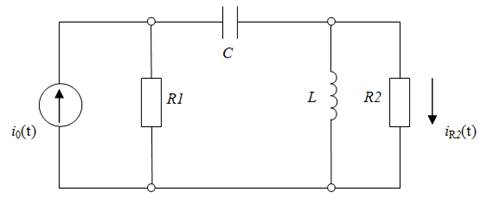
Рисунок 1 – Исходная схема электрической цепи

Исходные данные:

- i₀ (t) = 3 sin(t - 60 );

- L = 2 Гн;

- C = 3 Ф;

- R₁ = 4 Ом;

- R₂ = 5 Ом.

Преобразуем схему, что облегчит её анализ и сделает более наглядной для расчета тока. На рисунке 2 приведена эквивалентная исходной схема. Областью с пунктирными границами показано некое сопротивление Z_об, эквивалентное тому, что будет позже рассчитано в охватываемом участке ветви.

Рисунок 2 – Эквивалентная исходной схема

Здесь i₀ (t) – ток источника тока, описанный уравнением

i₀ (t) = 3 sin(t - 60 ), (2)

где i₁ – ток в ветви с сопротивлением R₁;

i₂ – ток, протекающий по участку с эквивалентным сопротивлением Z_об;

– ток на индуктивности L;

i_R2 (t) – искомый ток, текущий на сопротивлении R₂.

Для расчета и вывода итоговых формул будем применять метод комплексных амплитуд [1]. Суть метода заключается в том, что значения токов, напряжений и сопротивлений конкретных участков ветвей заменяются их комплексной формой. При этом действуют все законы и методы для расчета цепей. Если источник тока создает ток

i₀ (t) = I_m sin(ωt + φ), (3)

то его комплексное изображение имеет вид:

₀ = I_m cos(φ) + jI_m sin(φ), (4)

где I_m cos(φ) = λ – действительная часть числа;

I_m sin(φ) = ξ – мнимая часть числа;

j носит название мнимой единицы и характеризует значение квадратного корня из минус единицы.

С учетом приведенных выше обозначений получим алгебраическую форму записи комплексного числа

₀ = λ + ξ j. (5)

Также существует экспоненциальная форма записи комплексного числа:

₀ = I_m (6)

Операции дифференцирования и интегрирования заменяются умножением либо делением на jω. В итоге получается какая-либо система, в которой вместо интегрально-дифференциальных уравнений будут алгебраические уравнения, решаемые широко известными методами.

Сначала выведем формулы от значений, показанных на рисунке 2. Затем перейдем к комплексной форме. Применим закон Кирхгофа для токов и закон Ома для линейных цепей. По закону токов Кирхгофа из рисунка 2 имеем

i₀ (t) = i₁ (t) + i₂ (t). (7)

Эти токи текут в параллельных ветвях, а значит напряжения в этих ветвях одинаковы, тогда из закона Ома

U = IR (8)

следует, что

. (9)

Отсюда

i ₀ = 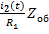. (10)

Z _об равно сумме емкостного сопротивления X_c и сопротивления участка с параллельными токами i_R2(t) и i_xl Z₁. Z₁ по правилу расчета при параллельном соединении, находится как

Z₁ = , (11)

где - индуктивное сопротивление.

Окончательно для Z _об имеем

Z _об = + X_c. (12)

Тогда ток i₂ может быть выражен как

i ₂ = (13)

Аналогично ток на индуктивности i_xl и ток на сопротивлении R₂ так же текут параллельно и для этих двух ветвей выполняется соотношение

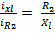, (14)

откуда получим

= . (15)

Также по закону токов Кирхгофа для токов i_xl и i_R2, i₂ выполняется

i₂ (t) = i_xl (t) + i_R2 (t). (16)

Из (12) и (13) получим

i_R2 (t) = 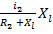(17)

В итоге из (10) и (14) получаем конечную формулу для искомого тока i_R2 (t)

i _R2 (t) = 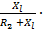(18)

Здесь для простоты вида формулы оставлено обозначение , которое находится по формуле (12).

Дата добавления: 2015-09-05