Модель гибридной системы

Модель гибридной системы (комбинации непрерывной и дискретной системы) дана в файле mixedm.m. Рассматриваемая S-функция моделирует систему, состоящую из последовательно включенных интегратора (1/s) и блока задержки (1/z). Особенность S-функции для гибридной системы в том, что вызов callback-методов для расчета дискретной части системы выполняется в те же моменты времени, что и для непрерывной ее части, поэтому пользователь, при написании S-функции, должен предусмотреть проверку правильности вызова callback-методов рассчитывающих дискретную часть системы.
Ниже приведен текст этой S-функции.

S-функция dsfunc:

function [sys,x0,str,ts] = mixedm(t,x,u,flag) % MIXEDM Пример S-функции. S-функция моделирует систему, состоящую из% последовательно включенных интегратора (1/s) и блока задержки (1/z).%% Шаблон для создания S-функции - файл sfuntmpl.m. %% Copyright 1990-2001 The MathWorks, Inc.% $Revision: 1.27 $% Авторский перевод комментариев: Черных И.В.% Шаг модельного времени и смещение для дискретной части системы: dperiod = 1; doffset = 0;switch flag % В зависимости от значения переменной flag происходит % вызов того или иного метода:%===============%% Инициализация %%===============% case 0 [sys,x0,str,ts]=mdlInitializeSizes(dperiod,doffset); %====================%% Расчет производных %%====================% case 1 sys=mdlDerivatives(t,x,u); %============================================================%% Расчет значений вектора состояний дискретной части системы %%============================================================% case 2, sys=mdlUpdate(t,x,u,dperiod,doffset); %===========================================%% Расчет значений вектора выходных сигналов %%===========================================% case 3 sys=mdlOutputs(t,x,u,doffset,dperiod); %====================%% Завершение расчета %%====================% case 9 sys = []; %======================================%% Неизвестное значение переменной flag %%======================================% otherwise error(['unhandled flag = ',num2str(flag)]); end % Окончание mixedm %===============================================================%% mdlInitializeSizes %% Функция инициализации %% Расчет начальных условий, значений вектора модельного времени,%% размерности матриц %%===============================================================% function [sys,x0,str,ts]=mdlInitializeSizes(dperiod,doffset)sizes = simsizes;sizes.NumContStates = 1; % Число непрерывных переменных состояния. sizes.NumDiscStates = 1; % Число дискретных переменных состояния. sizes.NumOutputs = 1; % Число выходных переменных (размерность выходного % вектора). sizes.NumInputs = 1; % Число входных переменных (размерность входного % вектора). sizes.DirFeedthrough = 0; % Прямой проход. Прохода входного сигнала на выход % нет. sizes.NumSampleTimes = 2; % Размерность вектора шагов модельного времени. % Шаги модельного времени задаются для непрерывной % и для дискретной частей системы. sys = simsizes(sizes);x0 = zeros(2,1); % Задание вектора начальных значений переменных % состояния. % Начальные условия нулевые str = []; % Параметр заразервирован для будущего % использования. ts = [0 0]; % Шаг модельного времени для непрерывной части % системы. dperiod doffset]; % Шаг модельного времени для дискретной части % системы.% Окончание mdlInitializeSizes %%========================================================================%% mdlDerivatives %% Функция для расчета значений производных вектора состояния непрерывной %% части системы %%========================================================================% function sys=mdlDerivatives(t,x,u)sys = u; % Окончание mdlDerivatives %=========================================================================%% mdlUpdate %% Функция для расчета значений вектора состояния дискретной части системы %%=========================================================================%% function sys=mdlUpdate(t,x,u,dperiod,doffset) % Расчет значения переменной состояния дискретной части системы% выполняется в соостветствии с дискретным шагом расчета% (погрешность по времени выбрана равной 1e-15). if abs(round((t - doffset)/dperiod) - (t - doffset)/dperiod) < 1e-15 sys = x(1);else sys = [];end % Окончание mdlUpdate %%========================================================% % mdlOutputs %% Функция для расчета значений вектора выходных сигналов %%========================================================% % function sys=mdlOutputs(t,x,u,doffset,dperiod) % Расчет значения выходного сигнала системы% выполняется в соостветствии с дискретным шагом расчета% (погрешность по времени выбрана равной 1e-15).% Если условие, заданное оператором if истинно, то выходной сигнал блока% изменяется. В противном случае выходной сигнал остается равным значению% на предыдущем шаге.% if abs(round((t - doffset)/dperiod) - (t - doffset)/dperiod) < 1e-15 sys = x(2);else sys = [];end % Окончание mdlOutputs

Пример модели с S-функцией mixedm приведен на рис.16.7.

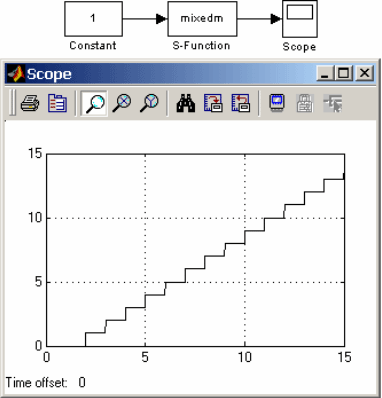
Рис. 16.7 Модель с S-функцией mixedm

[Скачать пример]

Дата добавления: 2015-09-05