|
Читайте также: |
Двигатель постоянного тока независимого возбуждения (рис. 16.9), описывается следующей системой дифференциальных и алгебраических уравнений в абсолютных единицах:
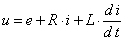
| (1) |
| (2) |
| (3) |
| (4) |
где
u - напряжение на якорной обмотке двигателя, e - электродвижущая сила (ЭДС) якоря, i - ток якоря, Ф - поток, создаваемый обмоткой возбуждения, M - электромагнитный момент двигателя, MС - момент сопротивления движению, 
- скорость вращения вала двигателя, R - активное сопротивление якорной цепи, L - индуктивность якорной цепи, J - суммарный момент инерции якоря и нагрузки, С - коэффициент связи между скоростью и ЭДС, СМ - коэффициент связи между током якоря и электромагнитным моментом.
|
| Рис. 16.9 Двигатель постоянного тока с независимым возбуждением. |
С точки зрения будущей модели, входными воздействиями являются напряжения якоря u и момент сопротивления движению MС, выходными переменными - электромагнитный момент двигателя M и скорость вращения вала двигателя , а переменными состояния - переменные стоящие под знаком производной: ток якоря i и скорость вращения вала двигателя . Остальные переменные, входящие в состав уравнений (1) - (4) являются параметрами, численные значения которых, необходимо будет задавать при проведении расчетов.
Преобразуем дифференциальные уравнения (1) и (2) к явной форме Коши и выполним подстановку. Система уравнений примет вид:
| (5) |
| (6) |
| (7) |
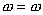
| (8) |
Последнее уравнение есть отражение того факта, что переменная состояния является также и выходной переменной.
Введем "машинные" переменные. Входные переменные: 
,. 
. Выходные переменные: 
,. 
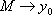, Переменные состояния: 
, 
.
Тогда уравнения (5) - (8) примут вид:
| (9) |
| (10) |
| (11) |
| (12) |
Перепишем систему уравнений в матричной форме:
| (13) |
| (14) |
где
 ,
|  ,
|  .
|
Отметим, что в получившейся системе уравнений входные переменные не участвуют в формировании выходных переменных (матрица обхода D - отсутствует) и, следовательно, параметр sizes.DirFeedthrough, определяемый при инициализации S-функции должен быть задан равным нулю.
Дата добавления: 2015-09-05; просмотров: 162 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Модель дискретной системы с переменным шагом расчета | | | Пример S-функции для ДПТ НВ |