Акустические системы и электроакустические аналоги

Акустические колебательные системы являются частными случаями систем механических. Обычно состояние механической системы характеризуется смещением и колебательной скоростью отдельных материальных точек. Воздействие характеризуется силами, действующими на систему.

Если линейная система совершает вынужденные колебания под действием внешней периодической синусоидальной силы, уравнение движения можно представить в виде:

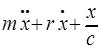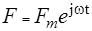= . (3)

Пусть r – активное сопротивление системы и на резонатор действует периодическое внешнее давление падающей звуковой волны .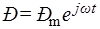

Уравнение движения (3) принимает при этом вид

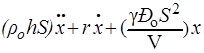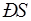= . (4)

Акустические системы удобнее описывать, пользуясь объемными смещениями и объемными скоростями, а за внешнее воздействие принимать давлением.

Введем в (4) объемные переменные: смещение , скорость 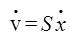и ускорение .

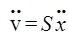Разделив обе части на 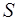, получим:

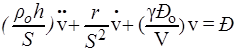
или

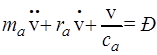. (5)

Коэффициенты при переменных этого уравнения называются акустическими параметрами системы. К ним относятся:

1) акустическая масса = = ;

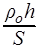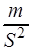2) акустическая гибкость = = ;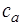

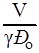3) акустическое сопротивление = .

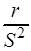Уравнение (5) аналогично уравнению, описывающему колебательные процессы в электрическом контуре:

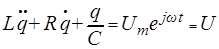. (6)

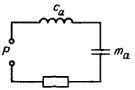Таким образом, аналогом резонатора Гельмгольца является электрический контур с последовательно соединенными параметрами , , 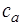. Установленная связь позволяет применять метод аналогий для анализа и синтеза сложных акустических систем.

Если решить уравнение (5) для стационарного режима относительно объемной скорости 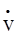(эту величину иногда называют потоком), то получим решение вида:

= ,

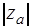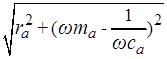или, в комплексной форме,

= .

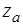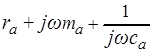Величина 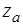называется полным акустическим сопротивлением и имеет те же составляющие (инерциальную, упругую, активную), что и механическое сопротивление .

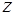Связь между акустическим и механическим сопротивлениями определяется формулой = .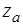

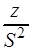Практическим свойством резонатора является его способность к усилению звука. Усиление резонатора (М) характеризуется отношением максимального давления 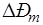в полости резонатора к максимальному (амплитудному) значению давления 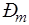в падающей звуковой волне:

.

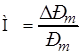Избыточное давление в полости значительно больше внешнего избыточного давления, а это означает, что вблизи от резонанса система дает значительное усиление акустического процесса, отбирая большое количество энергии от падающей на резонатор волны.

Процессы, происходящие в резонаторе Гельмгольца, связаны с упругой деформацией воздушного объема в полости (см. рис. а). Рассмотрим другой случай – колебание воздуха в открытой трубе длиной l и внутренним диаметром 2 a (см. рис. б).

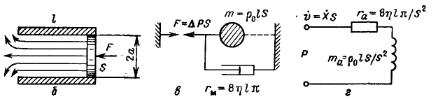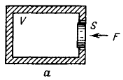
В отличие от резонатора Гельмгольца, воздух в открытой трубе не будет деформироваться. «Столб» воздуха смещается как единое целое вместе с поршнем. Характер возникающей при этом реакции обусловлен инерцией воздуха, смещаемого поршнем. Поэтому при вычислении этой реакции следует учесть массу воздуха в трубе:

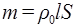, где .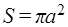

Кроме того, в колебаниях будет принимать участие воздух, непосредственно примыкающий к открытому концу трубы. Его инерция может быть учтена путем добавления к массе воздуха в трубе, так называемой массы «соколеблющегося» воздуха 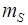, которую можно оценить по формуле:

~ .

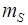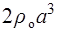Следовательно, общая масса воздуха, смещаемая поршнем,

М= .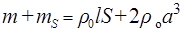

В случаях, когда длина трубы больше ее диаметра (l > 2 a), влиянием массы 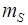можно пренебречь:

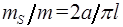< 1.

Таким образом, акустические системы можно изображать в виде механических схем с сосредоточенными параметрами (см. рис. в) и пользоваться для их расчета электромеханическими аналогами. При этом электрическим аналогом замкнутого воздушного объема является емкость, а движущегося потока воздуха в открытой трубе – индуктивность (см. рис. г).

Дата добавления: 2015-09-05