Резонатор Гельмгольца

Простейшая акустическая система с одной степенью свободы – так называемый резонатор Гельмгольца, представляет собой сосуд с коротким горлышком, заполненный воздухом.

При возбуждении резонатора звуковой волной воздух в горле резонатора колеблется, как поршень, а объем воздуха в полости резонатора (сосуде) создает необходимую упругость и обеспечивает возвращающую силу.

Таким образом, резонатор является колебательной системой с распределенными массой и упругостью.

Если размеры резонатора невелики по сравнению с длиной падающей волны (низкие частоты), то допустимо считать, что вся кинетическая энергия сосредоточена в слое воздуха, который движется в горле резонатора, а потенциальная энергия связана с упругой деформацией воздушного объема полости.

В этом предположении резонатор Гельмгольца является колебательной системой с одной степенью свободы, состоящей из сосредоточенных параметров массой m и упругостью с. Активное сопротивление r обусловлено трением воздуха о стенки трубы и потерями колебательной энергии, возникающими вследствие излучения звука открытым концом.

Сосредоточенные параметры системы определяются следующим образом. Рассмотрим характер реакции, создаваемой воздухом, заключенным в объеме резонатора V, при колебаниях невесомого поршня площадью S. Атмосферное давление Р _о.

Массу воздуха, движущегося в горле резонатора, можно определить как

,

где – высота горла, 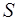– сечение горла резонатора, 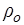– плотность воздуха.

Для определения гибкости воздушного объема в полости, представим, что воздушная пробка в горле смещается в сторону полости на величину х. Смещение невесомого поршня на расстояние х в сторону полости вызывает изменение объема на Δ V = – Sх и, следовательно, изменение давления в полости на величину Δ Р.

Если Р _о есть атмосферное давление, Δ Р – избыточное давление в полости и 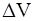– изменение объема V воздуха в полости, то при адиабатическом процессе (адиабатический процесс – это термодинамический процесс, при котором система не получает теплоты извне и не отдает ее. Быстропротекающие процессы, например, распространение звука, могут рассматриваться как адиабатический процесс)

(Р ₀ +Δ Р)(V+ Δ V) ^γ = Р ₀ V ^γ,

где γ = с_р/с_V – отношение удельных теплоемкостей, или показатель адиабаты.

Отсюда

или

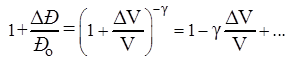
Если колебания являются малыми, т.е. , то последующие члены биноминального ряда можно отбросить. При этом, учитывая, что Δ V = – Sх, получаем

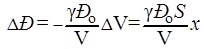– избыточное, или звуковое давление.

Тогда возвращающая сила или реакция воздуха, заключенного в полости,

(1)

Пропорциональность между и (по аналогии с законом Гука) свидетельствует об упругом характере реакции внутри полости. Таким образом, замкнутый воздушный объем акустической системы подобен пружине механической колебательной системы.

Из (1) можно определить акустическую гибкость (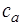) воздушного объема в полости как отношение смещения к возвращающей упругой силе :

, (2)

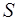где – атмосферное давление; – объем резонатора; – сечение горла резонатора; – плотность воздуха; – скорость распространения звуковой волны в воздухе, при температуре 20 ^оС, равная 340 м/с, 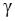– показатель адиабаты, равный 1,41

Дата добавления: 2015-09-05