
|
Читайте также: |
Работа 6
ИЗМЕРЕНИЕ ДОБРОТНОСТЕЙ ОБЪЕМНОГО РЕЗОНАТОРА
Цель работы
1. Изучение устройства закрытых объемных резонаторов и электромагнитных процессов в них.
2. Освоение методов измерений основных параметров резонатора (резонансной частоты и добротностей).
ПРЯМОУГОЛЬНЫЙ ОБЪЕМНЫЙ РЕЗОНАТОР
Объёмный резонатор, колебательная система сверхвысоких частот, аналог колебательного контура; представляет собой объём, заполненный диэлектриком (в большинстве случаев воздухом) и ограниченный проводящей поверхностью либо пространством с иными электрическими и магнитными свойствами. Наибольшее распространение имеют полые О. р. — полости, ограниченные металлическими стенками. Форма ограничивающей поверхности О. р. в общем случае может быть произвольной, однако практическое распространение (в силу простоты конфигурации электромагнитного поля, простоты расчёта и изготовления) получили О. р. некоторых простейших форм. К ним относятся круглые цилиндры, прямоугольные параллелепипеды, тороиды, сферы и др. Некоторые типы О. р. удобно рассматривать как отрезки полых или диэлектрических волноводов), ограниченные двумя параллельными плоскостями. Задача о собственных колебаниях электромагнитного поля в О. р. сводится к решению уравнений Максвеллас соответствующими граничными условиями. Процесс накопления электромагнитной энергии в О. р. можно пояснить на следующем примере: если между двумя параллельными отражающими плоскостями каким-либо образом возбуждается плоская волна, распространяющаяся перпендикулярно к ним, то при достижении одной из плоскостей волна полностью отразится от неё. Многократное отражение от обеих плоскостей приводит к образованию волн, распространяющихся в противоположных направлениях и интерферирующих друг с другом. Если расстояние между плоскостями L = n l/2 (l — длина волны, а n — целое число), то интерференция волн приводит к образованию стоячей волны (рис. 1),
амплитуда которой при многократном отражении сильно возрастает; в пространстве между плоскостями будет накапливаться электромагнитная энергия, подобно тому, как это происходит при резонансе в колебательном контуре.

Рис. 1. Образование стоячей волны в пространстве между двумя параллельными плоскостями в результате интерференции прямой и отражённых волн.
Свободные колебания в О. р. при отсутствии потерь энергии могут существовать неограниченно долгое время. Однако в действительности потери энергии в О. р. неизбежны. Переменное магнитное поле индуцирует на внутренних стенках О. р. электрические токи, которые нагревают стенки, что и приводит к потерям энергии (потери на проводимость). Кроме того, если в стенках О. р. есть отверстия, которые пересекают линии тока, то вне О. р. возбуждается электромагнитное поле, что вызывает потери энергии на излучение. Помимо этого, есть потери энергии в диэлектрике и потери за счёт связи с внешними цепями. Отношение энергии, запасённой в О. р., к суммарным потерям в нём за период колебаний, называется добротностью
О. р. Чем выше добротность, тем лучше качество О. р.
По аналогии с волноводами типы колебаний в О. р. классифицируются по группам в зависимости от того, имеет ли пространственное распределение электромагнитного поля осевые или радиальные (поперечные) компоненты. Колебания типа Н (или ТЕ) имеют осевую компоненту лишь магнитного поля; колебания типа Е (или ТМ) обладают осевой компонентой только электрического цоля. Наконец, у колебаний типа ТЕМ ни электрическое, ни магнитное поля не имеют осевых компонентов. Примером О. р., в котором могут возбуждаться колебания ТЕМ -типа, может служить полость между двумя коаксиальными проводящими цилиндрами, ограниченная с торцов плоскими проводящими стенками, перпендикулярными оси цилиндров.
Наиболее распространённым является цилиндрический О. р. Типы колебаний в цилиндрический О. р. характеризуют 3 индексами т, n, р, соответствующими числу полуволн электрического или магнитного поля, укладывающихся по его диаметру, окружности и длине (например, Етпр или Нтпр). Тип колебания (Е или Н) и его индексы определяют структуру электрического и магнитного полей в О. р. (рис. 2).

Рис. 2. Простейшие виды колебаний в круглом цилиндрическом полом резонаторе: а — E010, б — H111, в — H011. Сплошными линиями обозначены силовые линии электрического поля, пунктиром — силовые линии магнитного поля. Плотность силовых линий характеризует напряжённость поля. Для колебаний E010 и H111 плотность линий у оси цилиндра максимальна (пучность), а у его стенок равна нулю (узел). Силовые линии магнитного поля — замкнутые кривые.
Колебание Н011 цилиндрич. О. р. обладает особым свойством: оно безразлично к наличию контакта цилиндрических и торцовых стенок. Магнитные силовые линии этого колебания направлены так (рис. 2, в), что в стенках О. р. возбуждаются только токи, текущие по окружностям цилиндра. Это позволяет делать неизлучающие щели в боковых и торцовых стенках
О. р. Кроме цилиндрических О. р., применяются О. р. другой формы, например в лабораторных устройствах — прямоугольные О. р. (рис. 3, а). Важен О. р. тороидальной формы с ёмкостным зазором (рис. 3, б), применяемый в качестве колебательной системы клистрона. Особенностью основного типа колебаний такого О. р. является пространственное разделение электрического и магнитного полей. Электрическое поле локализуется главным образом в ёмкостном зазоре, а магнитное — в тороидальной полости.

Рис. 3. а — прямоугольный полый объёмный резонатор, в котором возбуждён основной тип колебаний E110; сплошные линии — силовые линии электрического поля, пунктир — магнитного поля; б — тороидальный резонатор клистрона; в — резонаторная система магнетрона.
Распределение поля в диэлектрическом О. р. при существенном различии в диэлектрической проницаемости диэлектрика и окружающего пространства близко к распределению поля в металлических полых резонаторах той же формы. В отличие от полых О. р., поле диэлектрических резонаторов проникает в окружающее пространство, однако быстро затухает при удалении от поверхности диэлектрика.
Металлические полые О. р. изготавливают обычно из металлов с высокой электропроводностью (Ag, Cu и их сплавы) или покрывают полость изнутри слоем Ag или Au. О. р. с чрезвычайно высокой добротностью получают из сверхпроводящих металлов. Настройка О. р. на определённую частоту производится изменением его объёма путём перемещения стенок или введения в полость О. р. металлических поршней, пластин и др. настроечных элементов. Связь с внешними цепями осуществляется обычно через отверстия в стенках О. р., с помощью петель, штырей и др. элементов связи. Для диэлектрических О. р. используются диэлектрики с высокой диэлектрической проницаемостью (рутил, тиганат стронция и др.), имеющие малые диэлектрические потери.
О. р. широко применяются в технике в качестве колебательных систем генераторов (клистронов, магнетронов и др.), фильтров, эталонов частоты, измерительных контуров, а также различных устройств для исследования твердых, жидких и газообразных веществ. О. р. применимы для частот 109—1011 гц. Для более высоких частот длина волны возбуждаемых в О. р. колебаний становится сравнимой с размерами неизбежных шероховатостей и отверстий в стенках О. р., что приводит к рассеянию электромагнитной энергии. Эта недостатки устраняются в открытых резонаторах, представляющих собой систему зеркал.
Резонансная частота колебаний или прямоугольного резонатора рассчитывается по формуле:

где a - длина резонатора вдоль оси X,
b - длина резонатора вдоль оси Y,
l - длина резонатора вдоль оси Z,
m - число вариаций поля по оси X,
n - число вариаций поля по оси Y,
p - число вариаций поля по оси Z,
c - скорость света,
ε - относительная диэлектрическая проницаемость заполнения,
- относительная магнитная проницаемость заполнения.
Составляющие колебания вычисляются следующим образом:
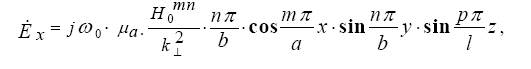
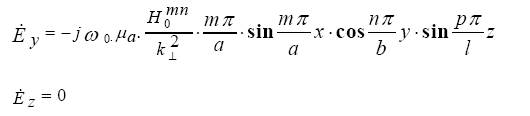


где  - поперечное волновое число.
- поперечное волновое число.
Составляющие векторов поля колебания типа 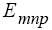 :
:
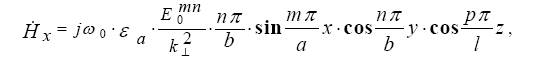

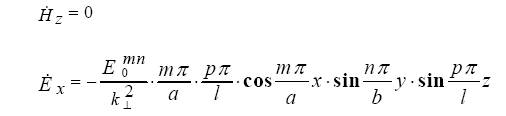


Добротность прямоугольного объемного резонатора:

,
где  - запасенная в резонаторе энергия электрического поля,
- запасенная в резонаторе энергия электрического поля,
 - запасенная в резонаторе энергия магнитного поля,
- запасенная в резонаторе энергия магнитного поля,

 - мощность потерь, обусловленная проводимостью заполняющего резонатор диэлектрика.
- мощность потерь, обусловленная проводимостью заполняющего резонатор диэлектрика.
 - мощность потерь, обусловленная
- мощность потерь, обусловленная
неидеальной проводимостью стенок резонатора. Интегрирование ведется по поверхности стенок резонатора.
 - активное поверхностное сопротивление
- активное поверхностное сопротивление
металла с проводимостью.
 - тангенциальная компонента магнитного поля вблизи стенки резонатора.)
- тангенциальная компонента магнитного поля вблизи стенки резонатора.)
Потери в резонаторе приводят к уменьшению запасенной энергии по закону:
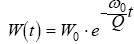 ,
,
где W0 - энергия резонатора в начальный момент времени t0.
Для пустого резонатора, работающего на колебании Н101, добротность
 .
.
Если резонатор заполнен диэлектриком с потерями, то результирующая добротность
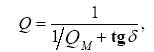 ,
,
где  - добротность резонатора, обладающего лишь потерями в металлических стенках;
- добротность резонатора, обладающего лишь потерями в металлических стенках;  - тангенс угла потерь вещества, заполняющего резонатор.
- тангенс угла потерь вещества, заполняющего резонатор.
Дата добавления: 2015-09-04; просмотров: 581 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача 2. | | | Методические указания по самоподготовке |