
Читайте также:
|
Прежде всего нужно определить "классическую алгебру событий". Под этим понимается непустое множество A, состоящее из подмножеств множества, такого, что для всех a,b A:
(1)  ,
,
(2)  .
.
Затем можно определить "аддитивное пространство вероятностей" (additiver Wahrscheinlichkeitsraum), имеющее место в классической алгебре событий A, путем введения вероятностной функции P, которая должна удовлетворять следующим условиям:
(3) P(a)>0, если a - непустое множество Ф,
(4) P() = 1,
(5) если ab=Ф, то P(ab)+P(a)+P(b).
Наконец, определяется "функция случайности" (эту функцию часто называют "случайной переменной", однако, Штегмюллер убедительно возражает против такого наименования) так, что, например, если мы обозначим "орла" монеты - 0, а "решку" - 1, и подбросим монету 3 раза, то можно сформулировать функцию случайности "числа орлов": (0,0,0)=3, (0,1,0)=2 и т.д. Таким образом, эта функция определена на множестве, а ее значениями являются действительные числа. С помощью мы можем вывести функцию распределения F, взяв вероятностную функцию P от множеств, полученных посредством функции случайности. Это можно записать следующим образом:

Таким образом, величины квантовой физики могут быть интерпретированы как функции случайности, где значение ожидания E функции распределения F выражается формулой:
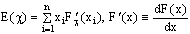 ,
,
Дата добавления: 2015-09-04; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Подход Миттельштедта | | | Для которой стандартное отклонение S представлено в виде |