Электроны - материальные частицы.

Каждая частица проходит либо через щель 1, либо через щель 2. Tertium non datur (TND).

Сторонники так называемой квантовой логики не испытывают каких-либо затруднений, отказываясь от первой предпосылки. Действительно, на основе именно этого эксперимента Юнг пришел к выводу о волновой природе света. Но они (по причинам, в которые мы здесь не станем входить) отказываются от второй предпосылки - принципа классической логики - и полагают, что логика должна быть модифицирована.

Теперь еще раз обратимся к прозрачной и легко интерпретируемой "трехзначной" логике Райхенбаха^[107]. "Трехзначной" он назвал ее потому, что в ней фигурирует третье значение - "неопределенно" - в дополнение к двум обычным значениям, которые приписываются высказываниям: "истинно" и "ложно". Райхенбах вводит следующую таблицу значений:

Таблица 1.

A		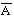~A	И - "истинно"
È	Í	Í	Н - "неопределено"
Í	È	Ë	Л - "ложно"
Ë	È	È

В первом столбце перечислены все три значения A. Во втором столбце определено отрицание A, обозначаемое 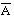; это отрицание не является, как в двузначной логике, строго контрадикторным по отношению к A. Отрицание, определенное таким образом, - произвольно выбранное определение, которое, как мы покажем, предназначено для выполнения замысла Райхенбаха - построить логическое исчисление, специально подобранное для квантовой механики. То же самое можно сказать о третьем столбце. Райхенбах называет отрицание, определенное в столбце 2, "полным отрицанием" ( 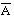), а отрицание в столбце 3 - "циклическим" отрицанием (~A).

При помощи этой таблицы затем определяются пропозициональные операторы, соответствующие "дизъюнкции" и "импликации" - аналогам одноименных операторов, которые фигурируют в обычных учебниках пропозициональной логики. Их можно свести в таблицу:

Таблица 2.

	А	В	Дизъюнкция А В	Альтернативная импликация А В
	И	И	И	И
	И	Н	И	Л
	И	Л	И	Л
	Н	И	И	И
	Н	Н	Н	И
	Н	Л	Л	И
	Л	И	И	И
	Л	Н	Н	И
	Л	Л	Л	И

Очевидно, что в строках 1,3,7 и 9 дизъюнкция совпадает с обычным определением. То же можно сказать об альтернативной импликации в тех же строках. В этих случаях A и B имеют только истинные и ложные значения.

Если теперь добавить к этой таблице определение эквиваленции: "Два высказывания эквивалентны, если оба истинны, оба ложны или оба неопределенны", то получим следующие эквиваленции в качестве тавтологий, то есть формул тождественно истинных в данной системе:

(3) .

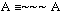(4) ,

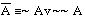(5) .

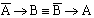(Если A - истинно в (3), то ~~~A также истинно, по таблице 1; если A - ложно, то ~~~A - также ложно; если A - неопределенно, то ~~~A также неопределенно. Следовательно, эта эквиваленция истинна в любом случае, то есть тождественно истинна. То же можно сказать о (4) и (5), применяя таблицу 2.

Дата добавления: 2015-09-04