
|
Читайте также: |
Для создания массива в Mathcad достаточно выполнить следующие действия:
- Установить курсор в то место, где надо создать матрицу;
- Щёлкнуть на кнопке математической панели Vector and Matrix Toolbar, а в появившейся панели инструментов щёлкнуть на кнопке Matrix or Vector. Также можно нажать комбинацию клавиш <Ctrl+m>;
- В появившемся диалоговом окне вписать число строк (Rows) и число столбцов (Columns), затем щёлкнуть ОК. На месте курсора появится шаблон матрицы;
- В каждое место ввода вписать число. Переход от одного места ввода в другое осуществляется с помощью клавиш со стрелками.
Для нумерации элементов массива используется нижний индекс. Для этого на математической панели существует кнопка  (Subscript). Также можно пользоваться клавишей <[> (открывающаяся квадратная скобка).
(Subscript). Также можно пользоваться клавишей <[> (открывающаяся квадратная скобка).
Чтобы из матрицы выделить вектор (один из столбцов) пользуются верхним индексом. Для этого нужно:
o Ввести имя матрицы и выделить его синим уголком курсора;
o В математическом меню щёлкнуть на кнопке Matrix and Vectors Toolbar и на кнопке  Vatrix Column;
Vatrix Column;
o В появившемся месте ввода набрать номер столбца.
Решение систем линейных алгебраических уравнений (СЛАУ)
В Mathcad легко реализуется вычисление обратной матрицы.
Для нахождения матрицы, обратной к заданной можно выбрать на панели Matrix значок  .
.
Поэтому первый метод решения СЛАУ — это метод обратной матрицы.
Второй способ решения СЛАУ — это использование процедуры lsolve.
Которая реализуется следующим образом:
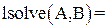 ,
,
где  — матрица коэффициентов,
— матрица коэффициентов,  — вектор-столбец свободного члена.
— вектор-столбец свободного члена.
Рассмотрим пример решения физической задачи с применением теории матриц.
Пример 1. С помощью первого и второго законов Кирхгофа для цепи со схемой, изображенной на рис.1, найти все токи ветвей.

Рис.1
Параметры цепи:  Ом,
Ом,  Ом,
Ом,  Ом,
Ом,  Ом,
Ом, 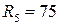 Ом,
Ом,  Ом,
Ом,  В,
В,  В,
В,  В,
В,  А,
А,  А,
А, 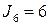 А.
А.
Решение
В данной задаче неизвестными являются токи, протекающие в ветвях, содержащих сопротивления. К таким ветвям относятся: ветвь с сопротивлением  (по ней протекает ток
(по ней протекает ток  ), ветвь с сопротивлением
), ветвь с сопротивлением 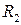 (по ней протекает ток
(по ней протекает ток  ), ветвь с сопротивлением
), ветвь с сопротивлением  (по ней протекает ток
(по ней протекает ток 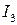 ), ветвь с сопротивлением
), ветвь с сопротивлением  (по ней протекает ток
(по ней протекает ток  ), ветвь с сопротивлением
), ветвь с сопротивлением  (по ней протекает ток
(по ней протекает ток  ), ветвь с сопротивлением
), ветвь с сопротивлением  (по ней протекает ток
(по ней протекает ток  ). В ветвях, содержащих источники тока
). В ветвях, содержащих источники тока  ,
,  и
и  токи заданы и равны соответственно
токи заданы и равны соответственно  ,
,  и
и  .
.
Таким образом, число неизвестных токов равно шести.
Поэтому для решения задачи необходимо получить шесть уравнений: три уравнения по второму закону Кирхгофа и три уравнения по первому закону Кирхгофа.
Первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю.
Число узлов в схеме равно восьми.
Условно будем полагать положительно направленными токами те, которые вытекают из узла, а отрицательно направленными — те, которые втекают в узел.
Второй закон Кирхгофа: сумма падений напряжений на сопротивлениях в контуре равна сумме ЭДС, входящих в данный контур.
Направления токов в ветвях указаны на рис.1 (в общем случае эти направления можно задавать произвольно).
Направление обхода контуров зададим единым образом для всех контуров: а именно, по часовой стрелке.
Тогда получим следующую систему уравнений (первые четыре уравнения записаны по второму закону Кирхгофа, последние три уравнения записаны по первому закону Кирхгофа).

Систему уравнений можно записать в матричном виде:

где 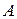 — матрица коэффициентов,
— матрица коэффициентов, 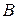 — вектор-столбец свободного члена,
— вектор-столбец свободного члена,  — вектор-столбец неизвестных токов.
— вектор-столбец неизвестных токов.
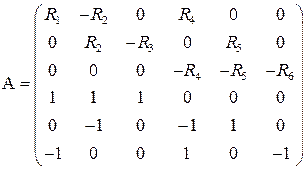 .
.
 .
.
 .
.
Чтобы получить искомое решение задачи достаточно задать в Mathcad матрицу и вектор-столбец свободного члена. Далее решить систему уравнений одним из указанных выше способов.
Для проверки полученных результатов необходимо произвести расчёт мощностей, выделяемых на резисторах и генерируемых источниками. Подтверждением правильности расчётов будет выполнение баланса мощностей, то есть:
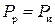 ,
,
где
 — мощность, выделяемая на резисторах (
— мощность, выделяемая на резисторах ( — число ветвей, содержащих резисторы);
— число ветвей, содержащих резисторы);
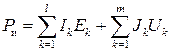 — мощность, генерируемая источниками (
— мощность, генерируемая источниками ( — число ветвей, содержащих источники ЭДС;
— число ветвей, содержащих источники ЭДС;  — число ветвей, содержащих источники тока;
— число ветвей, содержащих источники тока; 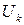 — напряжение между точкой, в которую втекает ток источника тока и точкой, из которой вытекает ток источника тока).
— напряжение между точкой, в которую втекает ток источника тока и точкой, из которой вытекает ток источника тока).
Решение поставленной задачи в Mathcad выглядит следующим образом.

Дата добавления: 2015-08-27; просмотров: 113 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тема 8. Межбюджетные отношения, их составляющие. | | | Задание 5.1. Рассчитать токи в ветвях. Проверить баланс мощностей. |