Графы и деревья

Многие структуры, представляющие практический интерес в информатике, могут быть представлены графами. Понятия теории графов используются в сетях, операционных системах и компиляторах. В качестве моделей графы удобно использовать в тех случаях, когда рассматривается система каких-либо объектов, между которыми существуют определенные связи, отношения, когда изучается структура системы, возможности ее функционирования. Множество самых разнообразных задач естественно формулируется в терминах графов. Так, например, могут быть сформулированы задачи составления расписаний в исследовании операций, анализа сетей в электротехнике, установления структуры молекул в органической химии, сегментации программ в программировании, анализа цепей Маркова в теории вероятностей.

Граф состоит из множества вершин и множества ребер, которые соединяют между собой вершины. С точки зрения теории графов не имеет значения, какой смысл вкладывается в вершины и ребра. Вершинами могут быть населенными пункты, а ребрами дороги, соединяющие их, или вершинами могут являться подпрограммы, соединение вершин ребрами означает взаимодействие подпрограмм. Часто имеет значение направления дуги в графе. Если ребро имеет направление, оно называется дугой, а граф с ориентированными ребрами называется орграфом.

Таким образом, граф — это совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра.

Граф G = (V, Е) задается парой конечных множеств V и Е. Элементы первого множества v1, v2,..., vM называются вершинами графа. Элементы второго множества el, e2,..., eN называются ребрами. Каждое ребро определяется парой вершин.

Если ребра графа определяются упорядоченными парами вершин, то такой граф называют ориентированным (на чертеже при изображении ориентированного графа на каждом ребре ставят стрелку, указывающую его направление).

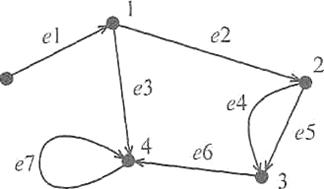
Рис.7 - Ориентированный граф с пятью вершинами и семью ребрами

Степенью вершины графа называется количество выходящих из нее ребер. Граф называется связным, если любая пара его вершин связана.

Если две вершины соединены двумя или более ребрами, то эти ребра называют параллельными (ребра е4 и е5). Если начало и конец ребра совпадают, то такое ребро называется петлей (ребро e7). Граф без петель и параллельных ребер называется простым.

Маршрут, в котором все определяемые им ребра различны, называют цепью. Цепь считаютзамкнутой, если ее концевые вершины совпадают. Замкнутая цепь, в которой все вершины различны, называется циклом.

Важным частным случаем графа является дерево, наиболее широко применяемое в программировании..

Существует довольно много равносильных определений деревьев, вот лишь некоторые из них.

Дерево - это связный граф без циклов.

Дерево - это связный граф, в котором при N вершинах всегда ровно N-1 ребро.

Дерево - это граф, между любыми двумя вершинами которого существует ровно один путь.

С точки зрения представления в памяти важно различать два типа деревьев: бинарные и сильноветвящиеся.

В бинарном дереве из каждой вершины выходит не более двух дуг. В сильноветвящемся дереве количество дуг может быть произвольным.

Дерево часто используют для изображения различных отношений (например, иерархических отношений).

Пример 10. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?

Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.

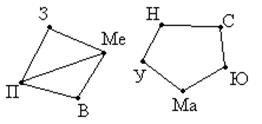
Теперь сразу видно, что долететь с Земли до Марса нельзя.

Дата добавления: 2015-08-27