Моделирование отношений между трофическими уровнями в биоценозах

Между видами существует связь, основанная на конкуренции за места обитания, за пищу и на «сожительстве» (например, лишайники как симбиоз грибов и водорослей). Широко распространена связь «паразит—хозяин», а также передача наследственных признаков через вирусы и бактериофаги (у бактерий).

В современной биологии одно из центральных мест занимают проблемы кооперативных эффектов и самоорганизации, соотношения «случая» и «необходимости». С появлением понятий биоценоза и биогеоценоза в биологических исследованиях стали применять методы математического моделирования, а использование ЭВМ для анализа процессов в сложных системах существенно обогатило науку о биосфере и экологию.

По распределению и численности видов имеется огромная информация, но ее нужно перевести на математический язык. Вводят «макроскопические характеристики», описывающие популяцию. Это число особей, соответствующее параметру порядка сложной системы. Оно «управляет» судьбой особей «в среднем». Если п — число особей (их плотность), то изменение п от скорости (числа) рождений g и числа смертей d можно записать как . В простейшем случае , где

коэффициенты не зависят от общей численности, а определяются доступностью пищи, климатическими условиями и т. п. Если эти внешние условия поддерживаются постоянными, то уравнение описывает растущую или убывающую по экспоненте популяцию. Значит, стационарного решения у этого уравнения нет, и рост не зависит от плотности, поэтому внешние условия должны зависеть от плотности. Наиболее важным из всех факторов, которые мы проигнорировали, вероятно, является истощение источников питания, который можно учесть введением

в уравнения члена (здесь предполагается, что пища поступает с постоянной скоростью). Тогда получается уравнение Ферхюльста:

При этом могут встретиться ситуации: «конкуренция—сосуществование»; «хищник—жертва»; «симбиоз». При сосуществовании различные виды не питаются одной и той же пищей, не поедают друг друга, размножаются в разных местах. Тогда уравнения для численности записываются как , . Ситуация усложняется, если виды живут или пытаются жить за счет одного и того же источника пищи или зависят от одних и тех же жизненных условий. Пример: растения, извлекающие фосфор из почвы. При этом одни растения закрывают листьями другие, лишая их солнечного света, или другой пример — птицы, которые строят гнезда в одних и тех же дуплах, и т.п. Математически это соответствует установлению генерации в лазере или автокаталитической реакции между двумя группами молекул. Решение показывает, что выживет только один тип, наиболее приспособленный. Это выживание может быть достигнуто улучшением индивидуальных констант и адаптацией. Если перекрываются источники пищи N, М:

где 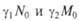— скорости поступления пищи; —

убыль пищи за счет внутренних причин типа гниения. Рассматривая правые части уравнений («силы») в плоскости п, т, можно найти условия, при которых возможно сосуществование. Обобщение на случай многих видов и источников пищи производится аналогично. Поэтому понятно, какую важную роль играют экологические ниши для выживания видов и почему виды так приспособлены к ним. Примером такого сосуществования служит распределение растительности по высоте, что изучается специально в биогеографии. Эта модель проста, но позволяет сделать оценки относительно динамики популяций при введении еще одного параметра, отвечающего за появление новых видев. Гены могут претерпевать мутации, образуя аллели. Мутации происходят случайно, но частота их может меняться под воздействием внешних факторов (повышение температуры, добавление химических агентов, ультрафиолетовое облучение и т.п.), поэтому можно считать, что мутации оказывают «мутационное давление», благодаря которому возникают особи новых типов. Новые свойства сначала будут рецессивными и только через несколько поколений станут доминантными. Пусть число особей новых типов, возникших из-за случайной мутации, равно и. Их показатели рождения и гибели иные, и новая популяция возникнет только при наличии флуктуации, которые будем описывать некой флуктуирующей силой и введем ее в уравнения роста популяций:

Пусть функция Fj(t) зависит от прежней популяции и факторов окружающей среды. Такие уравнения можно записать для разных типов, возникающих в системе. Так, система «подвидов» подвергается «давлению отбора», и это можно учесть, используя вышеприведенные уравнения, если считать, что условия окружающей среды (пища, например) остались прежними. Тогда для любого из подвидов, пользующихся тем же источником пищи, получим уравнение:

Если скорость мутаций у определенных видов мутантов мала, то выживут только наиболее приспособленные. Как отмечал Ха-кен, размножение видов можно заменить циклом А—В —С—..., который постулировался при описании эволюции макромолекул. Итак, возникновение новых видов благодаря мутациям (флуктуирующей силе) и отбору (вынуждающей силе) можно рассматривать как аналог неравновесного фазового перехода второго рода, т. е. аналогично процессам в лазере.

Модель Вольтерра—Лотки была одной из первых экологических моделей. В любом биоценозе происходит взаимодействие между всеми его элементами: особи одного вида взаимодействуют с особями и своего вида, и других видов. Эти взаимодействия могут быть мирными, а могут иметь связь типа «хищник-жертва». Было замечено, что численность хищных рыб колеблется в обратной пропорции относительно колебаний численности мелких рыбешек, которые служат им пищей. Анализ этих колебаний позволил математику Вито Вольтерра вывести (1926) уравнения, описывающие этот процесс. Если бы в биоценозе было только два вида (очень большое упрощение), то и в этом случае динамика численности каждого из видов сильно отличалась бы от картины их независимого существования.

Примером анализа таких структур может служить эволюция численности зайцев и волков, которая характеризуется колебаниями во времени. Изменение численности животных установлено по числу заготовленных шкурок. Абстрагируясь от различных обстоятельств, так или иначе влияющих на численность зверей, можно проанализировать важнейшую зависимость: зайцы едят траву, а волки — зайцев. Если бы жили одни зайцы и корма было достаточно, то их численность росла бы по экспоненциальному закону, а если бы жили только волки, то они вымирали бы. При их совместном существовании скорость изменения численности зайцев и волков связана с частотой их столкновений, т. е. пропорциональна количеству тех и других с некоторым коэффициентом. Уже эти соображения приведут к системе уравнений, и при определенных условиях система «хищник—жертва» придет в равновесие.

В случае неожиданной флуктуации (смерть волка или зайца, отстрел во время охоты и т.д.) равновесие нарушается и система приходит в движение. Она ведет себя как колебательная система, численности «хищников» и «жертв» начинают колебаться синфазно, с отставанием. Объяснение простое: рост численности зайцев приводит к увеличению питания для волков, но уменьшает количество травы, так что вскоре численность волков вырастает, а зайцев — уменьшается. Количество травы увеличивается, но запасы пищи для волков уменьшаются, и их численность падает. Тогда поголовье зайцев снова растет, и процесс повторяется. Режим колебаний с определенным периодом оказывается устойчивым. Такая система описывается уравнениями:

, где первое уравнение описывает количество жертв п, второе — количество хищников т. Эти уравнения имеют периодическое решение. Стационарное решение соответствует полному вымиранию, и оно единственное устойчивое. В природе такое может случиться, но биологи указывают на возможность животных-жертв найти убежище, не доступное хищникам, так что некоторая часть их выживет. Модель может усложняться введением нескольких типов жертв, которыми может питаться один хищник, и другими вариантами.

Ситуация «симбиоз» тоже моделируется, как и ситуации «хищник—жертва» и «конкуренция—сосуществование». Симбиоз отражает кооперацию отдельных видов в борьбе за существование, когда один вид помогает или покровительствует другому (как, например, кооперация пчел или деревьев). Поскольку скорость размножения одного вида зависит от наличия другого, то, пренебрегая внутривидовым подавлением , имеем:

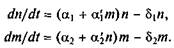
Здесь стационарный случай соответствует и = т = 0. В этих простых схемах не хватает очень многих факторов — смены климата и погоды, связи возраста особи и смертности, колебаний запасов пищи в разное время года и на разных территориях и т.д. Но использование даже простых моделей при разных, эмпирически учтенных тех или других параметрах дает интересные результаты.

Строя математические модели и проводя полевые испытания, ученые пытаются понять, каким образом паразиты и их хозяева коэволюционировали в тесные сообщества. Компьютерные модели этих процессов соответствуют «гонке вооружений» в ходе эволюции. Паразиты должны все время приспосабливаться, чтобы получить от хозяина больше ресурсов для роста своей популяции, а хозяин всячески старается этого не допустить. Биологи-эволюционисты считают, что существование полов с эволюционной точки зрения неудачно, и половые различия должны бы постепенно исчезнуть, но этого не происходит. Вероятно, потому, что пол является неким «секретным оружием», сохраняющим большую устойчивость хозяина: ведь паразит приспосабливается обычно к определенному его типу. Как только хозяева становятся жертвами, численность менее распространенных типов хозяев увеличивается, и наоборот. Исследования 90-х гг. XX в. показали, что бесполые рыбы чаще поражаются паразитами, чем разнополые. Те же результаты получены и на птицах — наличие паразитов наносит ущерб яркому оперению, и самки не выбирают таких самцов.

Созидательный характер симбиоза показала Л.Маргулис, исследуя роль естественного отбора в эволюции. Она предположила, что эукарио-тические клетки, имеющие внутренние органеллы, произошли от симбиоза более простых безъядерных клеток. Митохондрии и хлоропласты содержат иные гены, чем ядра клеток эукариот, но похожи на гены некоторых бактерий. Возможно, им не нужно было изобретать дыхание и фотосинтез методом «проб и ошибок». Большинство травоядных животных зависят от микроорганизмов, живущих в их кишечнике и переваривающих потребляемую животными клетчатку. Эволюционную схему, показывающую, как травоядные животные могли развиться от симбиоза их предков и микроскопических паразитов растений, очертил П. Прайс. Паразит приобрел способность производить ферменты для переваривания веществ, составляющих организм его хозяина-растения. Животное, вступив в симбиоз с паразитом, смогло использовать для себя продукты ферментации растительной массы. Успех в освоении новых пищевых ресурсов обеспечил преимущества в естественном отборе таких животных.

Жизнь даже небольшого озера невероятно сложна и многообразна, так что описать и «проверить алгеброй» эту достаточно простую систему почти невозможно, хотя такие попытки имеют место. Во многих странах разработаны системы моделирования гидробиоценозов — акватроны, соединенные напрямую с ЭВМ, которые сами ведут наблюдения и подсчитывают объекты, т. е. система сама корректирует модель. Например, для учета химико-биологических превращений нужно знать интенсивность роста водорослей, фотосинтеза, смертность каждого вида, скорость разложения органического вещества. Конечно, такие разработки очень дороги, но в конечном счете обещают значительный экономический результат.

Химическое равновесие в биосфере опирается на биотический круговорот. Хотя отдельные циклы изучены недостаточно, ясно, что система находится на грани порядка и хаоса и может быть выведена из этого состояния неустойчивого равновесия даже малым воздействием. Ряд ученых (Л. Маршалл, М. И. Будыко, Л.Беркнер и др.) считают, что резкое уменьшение углекислоты в атмосфере с появлением фотосинтеза приводило к похолоданию и оледенению Земли и, естественно, к нарушению существовавших циклов. Собственно, это сейчас и делает индустриально вооруженный человек. Биосфера сформировалась по своему плану, без участия человека, и биогеоценозы пока еще находят резервы, чтобы справиться с вмешательством человека, но неизвестно, насколько их хватит.

Качественно новый этап развития биосферы начался с появлением человека в конце третичного периода, хотя сначала его деятельность мало отличалась от деятельности других существ. Беря у биосферы все необходимое, человек отдавал ей то, что могли использовать другие, т.е. включился в биотический круговорот. Добывание огня вьщелило человека из ряда других животных. При этом человек не только сумел расселиться в районы холодного климата, пережить оледенения и защититься от хищников, но и научился уничтожать органические остатки, заменив в чем-то микроорганизмы. Так с малых шагов началось ускоряющееся изменение равновесия в биосфере.

Дата добавления: 2015-08-27