
Читайте также:
|
1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  .
.
Тема III (динамика твердого тела)
III – 1. Что такое момент импульса?
1)  ; 2) мгновенное значение
; 2) мгновенное значение  ; 3)
; 3)  ; 4)
; 4)  .
.
III – 2. Вектор момента импульса 
1) параллелен вектору импульса 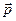 ;
;
2) параллелен радиусу-вектору  ;
;
3) перпендикулярен вектору 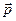 ;
;
4) перпендикулярен произведению  .
.
III – 3. Если  – радиус-вектор,
– радиус-вектор, 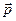 – импульс,
– импульс, 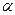 – угол между
– угол между  и
и 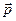 , то модуль момента импульса
, то модуль момента импульса  равен
равен
1)  , 2)
, 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
III – 4. Момент импульса – это
1) мгновенное значение импульса;
2) мгновенное значение изменения импульса;
3) векторное произведение радиуса-вектора на импульс;
4) скалярное произведение радиуса-вектора на импульс.
III – 5. В центрально симметричном поле сохраняется
1) только механическая энергия;
2) механическая энергия и импульс;
3) механическая энергия и момент импульса;
4) момент импульса и импульс.
III – 6. В центрально симметричном поле сила  подчиняется соотношению (
подчиняется соотношению (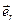 – единичный вектор, совпадающий по направлению с
– единичный вектор, совпадающий по направлению с  )
)
1)  ; 2)
; 2)  ; 3)
; 3) 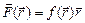 ; 4)
; 4)  .
.
III – 7. Момент импульса  и суммарный момент внешних сил
и суммарный момент внешних сил  связаны между собой соотношением
связаны между собой соотношением
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
III – 8. Вектор момента силы  равен
равен
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4) мгновенному значению силы.
; 4) мгновенному значению силы.
III – 9. При движении твердого тела, движение его центра масс подчиняется закону ( – равнодействующая внешних сил,
– равнодействующая внешних сил,  – равнодействующая всех сил)
– равнодействующая всех сил)
1) 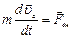 ; 2)
; 2) 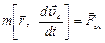 ; 3)
; 3)  ; 4)
; 4)  .
.
III – 10. При вращении вокруг неподвижной оси z уравнение динамики принимает вид (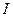 – момент инерции,
– момент инерции,  – момент сил,
– момент сил,  – угловая скорость)
– угловая скорость)
1) 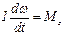 , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  .
.
III – 11. Проекция на неподвижную ось z момента импульса твердого тела, вращающегося с угловой скоростью 
1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  .
.
III – 12. При вращении вокруг неподвижной оси z, под действием силы 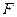 , имеющей момент
, имеющей момент  , угловое ускорение
, угловое ускорение  может быть найдено по формуле (
может быть найдено по формуле (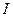 – момент инерции)
– момент инерции)
1) 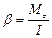 , 2)
, 2) 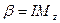 , 3)
, 3)  , 4)
, 4)  .
.
III – 13. Момент инерции материальной точки, имеющей массу  равняется (
равняется ( – радиус-вектор,
– радиус-вектор,  – расстояние до оси вращения)
– расстояние до оси вращения)
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 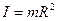 .
.
III – 14. Момент инерции 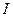 твердого тела, имеющего объем
твердого тела, имеющего объем  и массу
и массу  , вращающегося вокруг оси, находящегося на расстоянии
, вращающегося вокруг оси, находящегося на расстоянии  от центра масс, находится по формуле ( R - расстояние от оси вращения до элементарного объема dm )
от центра масс, находится по формуле ( R - расстояние от оси вращения до элементарного объема dm )
1)  , 2)
, 2) 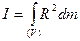 , 3)
, 3)  , 4)
, 4)  .
.
III – 15. По теореме Штейнера момент инерции тела массой m относительно произвольной оси, находящейся на расстоянии  от центра масс этого тела равен
от центра масс этого тела равен
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
III – 16. Для нахождения момента инерции твердого тела, имеющего объем  относительно его центра масс, применяется формула (
относительно его центра масс, применяется формула ( – расстояние от оси вращения,
– расстояние от оси вращения, 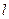 – толщина твердого тела)
– толщина твердого тела)
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 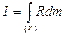 .
.
III – 17. Кинетическая энергия при вращении вокруг неподвижной оси Т равна
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
III – 18. Работа силы 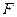 , имеющей момент
, имеющей момент  , при повороте на угол
, при повороте на угол  вокруг неподвижной оси с угловой скоростью
вокруг неподвижной оси с угловой скоростью  равен (
равен (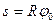 )
)
1)  ; 2)
; 2)  ; 3)
; 3) 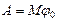 ; 4)
; 4) 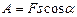 .
.
III – 19. Кинетическая энергия при плоском движении твердого тела, поступательная скорость которого 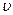 , а угловая скорость
, а угловая скорость  равен
равен
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
III – 20. При плоском движении выполняется соотношение
1)  ; 2)
; 2)  ; 3)
; 3) 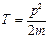 ; 4)
; 4)  .
.
III – 21. Момент инерции цилиндра относительно его оси ( – его масса,
– его масса,  – его радиус)
– его радиус)
1)  ; 2)
; 2) 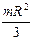 ; 3)
; 3)  ; 4)
; 4)  .
.
III – 22. Момент инерции стержня, вращающегося вокруг перпендикулярной ему оси, проходящий через один из его концов
1)  ; 2)
; 2) 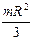 ; 3)
; 3) 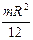 ; 4)
; 4)  .
.
III – 23. Момент инерции диска относительно перпендикулярной ему оси, проходящий через его край ( -радиус диска
-радиус диска  – его масса)
– его масса)
1)  ; 2)
; 2)  ; 3)
; 3) 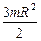 ; 4)
; 4)  .
.
III – 24. Если сосуд, наполненный водой, вращается вокруг некоторой оси, то при замерзании воды его момент инерции относительно этой оси
1) не изменится;
2) увеличится;
3) уменьшится;
4) уменьшится или увеличится в зависимости от расстояния от оси вращения до центра масс.
III – 25. Если с одной и той же горки высотой h скатываются труба и сплошной цилиндр одинаковой массы и радиуса без начальной скорости, то у подножия горки
1) скорость их будет одинаковой;
2) скорость цилиндра будет больше;
3) скорость трубы будет больше;
4) их кинетические энергии будут отличаться на 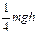 .
.
III – 26. Если на вращающейся платформе человек переходит с одного места на другое, то изменение угловой скорости от 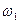 до
до  подчиняется соотношению (
подчиняется соотношению ( – момент инерции платформы,
– момент инерции платформы,  и
и  – момент инерции человека в начальном и конечном положении)
– момент инерции человека в начальном и конечном положении)
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
III – 27. Горизонтальный стержень может свободно вращаться вокруг вертикальной оси, проходящей через его центр. Масса стержня – М, длина – 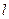 . В конец стержня попадает пуля, массой
. В конец стержня попадает пуля, массой  , летящая со скоростью
, летящая со скоростью 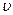 и застревает в стержне. Стержень начинает вращаться так, что его конец двигается со скоростью
и застревает в стержне. Стержень начинает вращаться так, что его конец двигается со скоростью  . Если
. Если  , то
, то  и
и 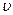 связаны соотношением
связаны соотношением
1)  ; 2)
; 2) 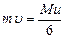 ; 3)
; 3)  ; 4)
; 4)  .
.
III – 28. Колесо в виде обода (масса распределена по образующей) скатывается с горки высотой h. Скорость колеса в начале  и в конце
и в конце  связаны между собой соотношением
связаны между собой соотношением
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
III – 29. При действии на вращающийся гироскоп силы, перпендикулярной оси вращения,…
1) ось сохраняет свое положение при небольшом изменении скорости вращения;
2) ось наклоняется в направлении силы;
3) ось поворачивается перпендикулярно приложенной силе;
4) ось поворачивается в сторону, противоположенную по направлению приложенной силы.
III – 30. В поле силы тяжести угловая скорость  прецессии волчка (гироскопа) массой
прецессии волчка (гироскопа) массой  связана с угловой скоростью его вращения
связана с угловой скоростью его вращения  и его моментом инерции I соотношением
и его моментом инерции I соотношением
1 ) 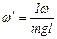 , 2)
, 2)  , 3 )
, 3 )  , 4)
, 4)  .
.
Дата добавления: 2015-08-27; просмотров: 182 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| II – 21. Действие неконсервативных сил приводит к тому, что | | | Тема IV |