Принципы стохастического доминирования

На практике определение функции полезности инвестора может оказаться не простым делом. Альтернативным подходом инвестиционного выбора служит принцип стохастического доминирования. Его особенность состоит в том, что он не требует точного знания функции полезности инвестора. Относительно функции полезности накладывается только следующее ограничение: она должна быть монотонной и не убывающей.

Портфель считался доминирующим, т.е. предпочтительным по сравнению с другими портфелями, если он имел более высокий уровень доходности при том же уровне риска или более низкий риск при той же ожидаемой доходности, чем другие портфели. Понятие доминирующего портфеля можно определить и относительно любого другого критерия, на основе которого инвестор будет осуществлять свой выбор. В рамках принципа стохастического доминирования в качестве такого критерия используется вероятностный подход. Первый портфель стохастически доминирует над вторым портфелем, если он показывает результаты не хуже второго портфеля и, по крайней мере в одном из вероятностных исходов, показывает лучший результат. Например, имеются два портфеля А и В. Инвестор прогнозирует десять возможных вероятностных сценариев. В девяти из них ожидаемые доходности портфелей равны, в одном из них доходность портфеля А больше доходности портфеля В. Тогда портфель А стохастически доминирует над портфелем В. Соответственно, инвестор сделает выбор в пользу портфеля А. Выделяют три порядка стохастического доминирования.

Стохастическое доминирование первого порядка предполагает, что инвестор предпочитает большее количество полезности меньшему количеству, т.е. его функция полезности возрастающая, соответственно .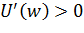

Рассмотрим два рискованных портфеля. Их доходность является случайной величиной, обозначим ее через r. Наименьшее и наибольшее значения доходности соответственно равны r₁ и r_n. Обозначим функцию распределения доходности первого портфеля через F, второго – через G. Приобретение каждого портфеля приносит инвестору определенный уровень полезности. Сравнивая их, инвестор должен выбирать тот из них, который обеспечивает ему большую ожидаемую полезность. Пусть первый портфель приносит инвестору большую ожидаемую полезность, т.е.:

Тогда с учетом функций распределения доходности портфелей неравенство эквивалентно:

Неравенство выдерживается в том случае, если:

1.

И

2. по крайней мере для одного r,

т.е. функция распределения G для каждого данного значения r имеет по крайней мере такое же или большее значение, чем функция распределения F. Таким образом, функция распределения доходности более предпочитаемого портфеля никогда не превосходит функции распределения доходности менее предпочитаемого портфеля.

Приведенные выше условия 1-2 являются условием стохастического доминирования первого порядка. Оно означает: вероятность того, что первый портфель принесет доходность меньше некоторого значения r меньше вероятностей того, что второй портфель принесет доходность меньше этого значения r. Другими словами, вероятность того, что доход составит величину меньше к меньше для первого портфеля, чем для второго. В этом случае инвестор всегда предпочтет первый портфель второму. Таким образом, первый портфель (вероятностное распределение F) доминирует над вторым портфелем (вероятностным распределением G) в рамках стохастического доминирования первого порядка.

Графически условие стохастического доминирования первого порядка проиллюстрировано на рисунке.

Рисунок 1. Стохастическое доминирование первого порядка

На рисунке функция распределения Fрасположена ниже функции распределения G для любого значения r. Поэтому первый портфель характеризуется меньшей вероятностью принести доход меньше чем второй портфель для любого значения r. Так, например, вероятностью того что доходность второго портфеля составит меньше величины r* равна 50%, а первого портфеля – только 25%.

Если, сравнивая активы, обнаружено условие 1-2, то анализ на этом прекращается, так как первый портфель предпочтительнее второго. Однако ситуация может оказаться не однозначной. На рисунке ниже представлен случай, когда функции распределения доходности первого и второго портфелей пересекаются.

Рисунок 2. Стохастическое доминирование второго порядка

Поэтому нельзя однозначно сказать, какой из портфелей предпочтительнее для инвестора. В этом случае оценку можно осуществить на основе стохастического доминирования второго порядка. Однако оно накладывает дополнительное ограничение на функцию полезности: она должна быть выпуклой вверх, т.е. добавляется условие не склонности инвестора к риску, что означает U”(w) < 0. Для стохастического доминирования второго порядка условие выдерживается в том случае, если:

для всех r

И

по крайней мере для одного r.

k располагается в интервале от r₁ до r_n.

Таким образом, критерий стохастического доминирования второго порядка основан на сравнивании не функций распределения доходности портфелей, а интегралов от этих функций, т.е. площадей под функциями распределения. Определим зависимость величины данной площади от значения r как накопленную функцию распределения. Тогда можно сказать, что первый портфель предпочтительнее второго, если накопленная функций распределения его доходности никогда не превосходит, и по крайней мере в одном случае меньше, накопленной функции распределения второго портфеля.

Доминирование второго порядка определяется для инвестора не склонного к риску, поэтому оно учитывает тот факт, что ценность единицы богатства для него выше для небольшого уровня богатства и уменьшается с его ростом. В результате инвестор должен в большей степени предпочесть портфель, для которого существует меньшая вероятность принести меньший доход на более нижнем участке распределения доходности, чем на более верхнем. Другими словами, инвестор больше теряет полезности от потери богатства на более нижнем отрезке распределения доходности, чем на более верхнем. В рамках стохастического доминирования второго порядка рассматривается инвестор не склонный к риску, поэтому оно имеет отношение к дисперсии доходности портфелей.

Как следует из условия доминирования второго порядка, доминирование первого порядка одного портфеля над другим автоматически предполагает его стохастическое доминирование и второго порядка. Таким образом, условие стохастического доминирования второго порядка является более слабым условием.

Критерий стохастического доминирования второго порядка может не дать ответа на вопрос о предпочтительности одного портфеля над другим. Тогда переходят к стохастическому доминированию третьего порядка, накладывая на функцию полезности еще одно ограничение: инвесторы характеризуются убывающей абсолютной несклонностью к риску, т.е. А’< 0. Данное условие выполняется, если третья производная функция полезности положительная, т.е. U’’’> 0. Данное условие можно получить следующим образом. Коэффициент абсолютной не склонности к риску равен:

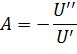
Его первая производная по богатству составляет:

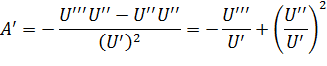
В правое части уравнения второе слагаемое является величиной положительной, поскольку стоит во второй степени. В пером слагаемом U’ > 0. Поэтому для выполнения условия А’ < 0 необходимо, чтобы U’’’ > 0. Еще одно условие доминирования третьего порядка состоит в том, что ожидаемая доходность первого портфеля больше ожидаемой доходности второго портфеля, т.е. инвесторы предпочитают распределения с большей правосторонней скошенностью.

Условие стохастического доминирования третьего порядка записывается как:

для всех r, и

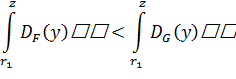
по крайней мере для одного r, где и , и z располагается в интервале от r₁ до r_n.

Если через D обозначить функцию, которая является накопленной функцией накопленной функции распределения (НФНФР), то можно сказать, что первый портфель предпочтительнее второго, если функция НФНФР его доходности никогда не превосходит, и по крайней мере в одном случае меньше, функции НФНФР доходности второго портфеля.

Если сравнить стохастическое доминирование со средне-дисперсионным анализом, то можно отметить, что стохастическое доминирование дает инвестору более общий подход к оценке рискованных портфелей.

Дата добавления: 2015-08-27