Работа с матрицами в MathCAD

Практическая работа № 3

В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами.

Предварительно матрицу нужно определить и ввести в рабочий документ MathCAD.

Для того чтобы определить матрицу, введите с клавиатуры имя матрицы и знак присваивания (<Shift>+<:>). Затем откройте панель операций с матрицами и нажмите кнопку «Создать матрицу или вектор» или выберите в меню Вставка (Insert) команду Матрицу (Matix). В окне диалога введите число строк и столбцов и заполните значениями поле ввода матрицы.

Большинство вычислений с матрицами, как и другие вычисления в MathCAD, можно выполнять тремя способами – с помощью панелей инструментов, выбором операции в меню или обращением к соответствующей функции.

За кнопками на панели инструментов Матрицы закреплены следующие функции:

· определение размеров матрицы

· X_n – ввод нижнего индекса

· X^-1 – вычисление обратной матрицы

· |X| - вычисление определителя матрицы: 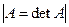; вычисление длины вектора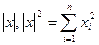

· поэлементные операции с матрицами: если 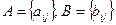, то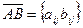

· M^<> – определение столбца матрицы: M^<j> - j-й столбец матрицы

· M^T – транспонирование матрицы: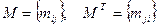

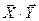· - вычисление скалярного произведения векторов: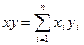

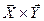· - вычисление векторного произведения двух векторов: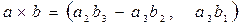

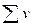· - вычисление суммы компонент вектора: ;

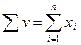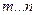· - определение диапазона изменения переменной

· визуализация цифровой информации, сохраненной в матрице.

Для того, чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно выделить матрицу и щелкнуть в панели по кнопке операции либо щелкнуть по кнопке в панели и ввести в помеченной позиции имя матрицы.

Функции, предназначенные для решения задач линейной алгебры, собраны в разделе Векторы и матрицы (Vector and Matrix); их можно разделить на три группы: функции определения матриц и операции с блоками матриц, функции вычисления различных числовых характеристик матриц и функции, реализующие численные алгоритмы решения задач линейной алгебры.

Функции определения матриц и операции с блоками матриц:

· matrix(m, n, f) – создает и заполняет матрицу размерности m x n, элемент которой, расположенный в i-ой строке, j-ом столбце, равен значению f(i,j) функции f(x,y);

· diag(v) – создает диагональную матрицу, элементы главной диагонали хранятся в векторе v;

· identity(n) – создает единичную матрицу порядка n;

· augment(A, B) – формирует матрицу, в первых столбцах которой содержится матрица A, а в последних – матрица B (матрицы A и B должны иметь одинаковое число строк);

· stack(A, B) – формирует матрицу, в первых строках которой содержится матрица A, а в последних – матрица B (матрицы A и B должны иметь одинаковое число столбцов);

· submatrix(A, ir, jr, ic, jc) – формирует матрицу, которая является блоком матрицы A, расположенным в строках с ir по jr и в столбцах с ic по jc (ir<=jr, ic<=jc).

Номер первой строки (столбца) матрицы или первой компоненты вектора хранится в MathCAD в переменной ORIGIN. По умолчанию в MathCAD координаты векторов, столбцы и строки матрицы нумеруются, начиная с 0 (ORIGIN:=0). Поскольку в математической записи чаще всего используется нумерация с 1, перед началом работы с матрицами будем определять значение переменной ORIGIN равным 1, т.е. будем, прежде всего, выполнять команду ORIGIN:=1.

Функции вычисления различных числовых характеристик матриц:

· last(v) – вычисление номера последней компоненты вектора V;

· length(v) – вычисление количества компонент вектора V;

· rows(A) – вычисление числа строк в матрице A;

· cols(A) – вычисление числа столбцов в матрице A;

· max(A) – вычисление наибольшего элемента в матрице A;

· min(A) – вычисление наименьшего элемента в матрице A;

· tr(A) – вычисление следа квадратной матрицы A (след матрицы равен сумме ее диагональных элементов);

· rank(A) – вычисление ранга матрицы A;

· norm1(A), norm2(a), norme(A), normi(A) – вычисление норм квадратной матрицы A.

Функции, реализующие численные алгоритмы решения задач линейной алгебры:

· rref(A) – приведение матрицы к ступенчатому виду с единичным базисным минором (выполняются элементарные операции со стоками матрицы);

· eigenvals(A) – вычисление собственных значений квадратной матрицы A;

· eigenvecs(A) – вычисление собственных векторов квадратной матрицы A; значением функции является матрица, столбцы которой есть собственные векторы матрицы A, причем порядок следования векторов отвечает порядку следования собственных значений, вычисленных функцией eigenvals(A);

· eigenvec(A, l) – вычисление собственного вектора матрицы A, отвечающего собственному значению l;

· lsolve(A, b) – решение системы линейных алгебраических уравнений Ax=b.

Вычисления с использованием описанных функций выполняются стандартным для MathCAD способом. Чтобы обратиться к функции, введите с клавиатуры имя функции, перечислите в скобках ее аргументы, введите знак равенства и щелкните по свободному месту в рабочем документе вне выделяющей рамки. Результат вычислений (число, вектор, матрица) будет отображен в рабочем документе справа от знака равенства.

Если предполагается использовать результаты в дальнейших вычислениях, им следует присвоить имя. Для этого введите с клавиатуры имя переменной и знак присваивания, а справа от него – имя функции со списком аргументов в круглых скобках. Если теперь ввести с клавиатуры имя переменной, знак равенства и щелкнуть по свободному месту в рабочем документе вне выделяющей рамки, то результат вычислений будет отображен справа от знака равенства.

Имя функции можно вставить из списка: щелкните по месту вставки, затем по строке Функция (Function) меню Вставка (Insert), выберите в окне списка стрелками прокрутки нужную функцию и подтвердите выбор щелчком по кнопке OK в окне диалога.

Вычисления могут производиться в двух режимах – автоматическом и последовательном. В первом случае операция выполняется сразу после ввода команды и щелчка по рабочему документу вне выделяющей рамки, во втором – после команды Вычислить (Calculate). Режим вычислений устанавливается в меню Математика (Math). По умолчанию включен режим автоматических вычислений.

MathCAD читает и выполняет введенные выражения слева направо и сверху вниз, поэтому следите, чтобы выражение для вычисления располагалось правее и ниже определенных для него значений переменных.

Дата добавления: 2015-08-27