i* vi. д. ц

можно рассуждать аналогично): искомая функция имеет вид у — = kx->f-b, однако значения параметров k и b пока неизвестны. При подстановке х — Х{ по формуле должно, было бы получиться kx^b, а в результате эксперимента получилось у/, т. е. формула дает расхождение у_{ — kx_t — Ь с экспериментом, полученное за счет оши­бок эксперимента и вычислений, неточной линейности изучаемой за­висимости и т. п. Эта разность между левой и правой частями формулы называется невйзкой. И вот k и b подбирают так, чтобы

п сумма квадратов этих невязок, т. е. S= ^ (у,- — kx_t — b)^z, была

i=i

минимально возможной. (Можно брать и сумму других четных сте­пеней или, например, сумму абсолютных величин невязок, но тогда вычисления будут значительно сложнее. Однако руководствоваться суммой самих невязок, конечно, нельзя, так как она может получить­ся малой при больших по абсолютной величине слагаемых разного знака.) Мы приходим к задаче на минимум функции S = S(k, b). Пользуясь необходимыми условиями (19), видим, что для минимума должно быть

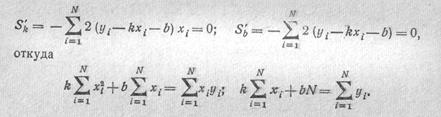
Для нахождения k к b получилась простая система двух урав­нений первой степени с двумя неизвестными, поскольку все х_; и y_t даны, которую легко решить. То, что здесь получится действительно минимум S, вытекает из смысла решаемой задачи.

Подобный метод применяется к подбору эмпирических формул • другого вида, а также и к иным задачам.

Рассмотрим такой пример. Пусть для определения некоторых величин х, у эмпирически выяснялись соотношения между ними, причем оказалось, что приближенно

С виду эта система противоречивая: сложив первые два уравнения, вступаем в противоречие с третьим. Однако возможны ведь ошибки эксперимента! По­этому постараемся удовлетворить системе (30) как можно точнее, чтобы сумма квадратов невязок оказалась как можно меньшей. Значит, надо найти такие к, у, для которых величина

5И* + 0-5,8)» + (* + 20.-8,1)«+ (2*-г-30-13,2)»

минимальна. Применение необходимого условия (19) дает

S'_x = 2 (x + y-5,8)-f 2 (* + 2у-8,1)Н-2(2х + 3(/—13,2)2 = 0; S^ = 2(x + i/—5,8) + 2(*-f-2# —8,1) 2+2 (2x+3</ —13,2)3 = 0.

Сокращая на 2, получим

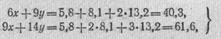
откуда, решая простейшим способом, получим * = 3,3, у = 2,3. Конечно, си-¹ стема (30) удовлетворяется этими значениями лишь приближенно. Естественно, чем больше соотношений вида (30) между х и у будет определено, тем досто­вернее получатся значения х и у, если нет

систематических ошибок эксперимента, так как при этом случайные ошибки в отдельных соотношениях погашают друг друга. Анало­гично решаются другие системы приближен­ных, в частности эмпирических, уравнений, если число уравнений больше, чем число неизвестных.

Метод наименьших квадратов, откры­тый французским математиком А. Лежанд-ром (1752 —1833) и Гауссом, в настоящее время имеет многочисленные приложения.

9. Кривизна поверхностей. Классифи­кация стационарных точек, указанная в п. 7, непосредственно связана с классифи­кацией поверхностей.

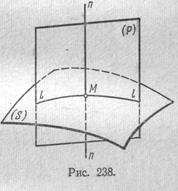
Рассмотрим произвольную поверхность (S) и на ней некоторую точку М (рис. 238).

Если провести через эту точку нормаль пп к поверхности, а затем через эту нормаль произвольную плоскость (Р), то эта плоскость пересечет (S) по некоторой линии //, нормальному сечению, которое имеет в точке М определенную кривизну /г (п. VII.24). 'Если теперь поворачивать пло­скость (Р) вокруг нормали пп, то нормальное сечение будет меняться и поэтому величина k тоже, вообще говоря, будет меняться. Чтобы выяснить закон этого изменения, выберем систему декартовых координат так, чтобы начало координат находилось в точке М, а ось z пошла по нормали пп. Тогда вблизи М уравнение поверхности (S) можно представить в виде z = •=z(x, у), причем значение z (О, 0) будет стационарным (почему?). Рассуждая, как в конце п. 7, мы получим, что после некоторого поворота осей коорди­нат вокруг пп уравнение (S) примет вид

z = —(Х,!д;'²-1-Я₂{/'²) + члепы высшего порядка малости. (31)

Пусть плоскость (Р) образует с плоскостью x'Mz угол ср; тогда, переходя к полярным координатам, получим *' = pcos(p, {/' = psincp, откуда z =

¹⁼³ ~п (^i cos² ф + Х₂ sin²q>) р²+ •• •, т. е. в точке М будет • р = 0,.-t-j=i

= X, со8²<р + Я₂ sin²cp. По формуле (VII.37) получаем искомое выражение для кривизны fe= | A,! cos² Ф + А.2 sin² ф |. При этом возможны следующие случаи (три типа точек у поверхностей):

1. Пусть A,_tX₂ > 0, т. е. Xj и К₃ имеют одинаковый знак. Тогда все нор­мальные сечения вблизи М выгнуты в одну сторону, причем величина k заключена между | Xj | и | Я,₂ |, причем ft= 17ц | для <р = 0, т. е. для плоско-

сти х'Мг, и /г = |А,₂| для 9 = -^-, т. е. для плоскости у'Мг (это — главные

нормальные сечения). Такая точка М называется эллиптической (а при |^jl = |Xj|— сферической) точкой поверхности (S); например, у эллипсоида или у двуполостного гиперболоида все точки эллиптические. Как видно из уравнения (31), касательная плоскость к (S) в точке М имеет вблизи /И с (S) только одну общую точку М; параллельные ей плоскости сначала дают в пересечении с (S) бесконечно малый эллипс, оси которого располо­жены по главным нормальным сечениям, а затем форма сечения может стать более сложной (рис. 239, а).

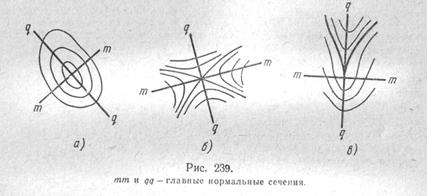
2. Пусть XjXj < 0. Тогда некоторые нормальные сечения выгнуты вблизи М в одну сторону и имеют в М положительную кривизну, а некото­рые—в другую сторону и также имеют в М положительную кривизну; так будет, например, для точек однополостного гиперболоида. Среди первых нормальных сечений одно имеет наибольшую кривизну | К_г \, а среди вто­рых—одно имеет наибольшую кривизну | Я₂ |. Эти главные нормальные сечения также взаимно перпендикулярны. Точка М называется гиперболиче­ской. Касательная плоскость к (S) в точке М пересекает (S) по двум ли­ниям, пересекающимся в М под положительным углом; бесконечно близкие параллельные к ней плоскости дают в пересечении в бесконечной близости М гиперболы с осями по главным нормальным сечениям (рис. 239, б).

3. Пусть Х₁Я₂ = 0. Тогда если ki и Х₂ не оба равны нулю, то все нор­мальные сечения выгнуты вблизи М в одну сторону и имеют в /И положи­тельную кривизну, но одно имеет нулевую кривизну в М, а перпендикуляр­ное сечение имеет и М наибольшую кривизну. Точка называется параболиче­ской; например, у цилиндрической или конической поверхности все точки параболические. Типичная картина пересечений (5) с плоскостями, парал­лельными касательной плоскости в М, показана на рис. 239, в, но довольно часто бывают и другие картины. К этому же типу принадлежит и тот случай, когда Х₁ = Х₂ = 0, т. е. ft = 0 при всех ср, такие точки называются точками уплощения поверхности (S), так как ясно, что у плоскости все точки будут такими.

В приведенных примерах поверхностей все точки имели одинаковый тип. Но это необязательно, например, у тора, т. е. бублика идеальной формы, имеются точки всех трех типов (где они?).

Во всех случаях произведение К]\₂ называется полной (гауссовой) кри­визной поверхности (S) в точке М. Полная кривизна обладает тем замеча­тельным свойством, что когда поверхность изгибается без растяжений, то эта кривизна не меняется. Например, если лист бумаги изогнуть произволь-

ным способом, то полученная поверхность будет иметь в каждой своей точке нулевую полную кривизну. По этой же причине никакой кусок сферы нельзя разложить на плоскости без деформаций, т. е> невозможны географические карты без искажений.

Поверхность может иметь особые точки (ими обычно служат или изоли­рованные точки, или «конические» точки, как вершина у кругового конуса, хотя бывают особые точки и гораздо более сложного вида), а также целые особые линии (это чаще всего изолированные линии или линии самопересече­ния; бывают также «ребра возврата» и другие виды). Часто рассматриваются поверхности «с краем», т. е. вырезанные из более полной поверхности напо­добие куска плоскости или куска сферы.

10. Условный экстремум. В задачах, рассмотренных в п. 7, независимые переменные не были связаны между собой никакими соотношениями; такой экст-

ремум называется безуслов­ным. Встречаются также за­дачи на условный экстре­мум, в которых независи­мые переменные связаны между собой соотношения­ми, имеющими вид равенств. Начнем с функций двух пе­ременных.

Пусть ищется макси­мум или минимум функции z—f(x, у) при условии, что переменные х и у свя­заны соотношением

F(x, i/)-/i. (32)

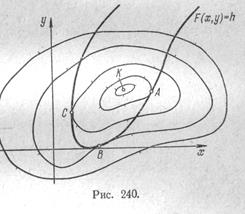
Это означает, что значения функции / рассматриваются и сравни­ваются только для точек (в плоскости аргументов), лежащих на линии с уравнением (32). Например, на рис. 240, где изображены линии уровня некоторой функции /, безусловный максимум дости­гается в точке К, тогда как условных экстремумов три: два мак­симума в точках Л и С и один минимум в точке В (почему?). Безусловный максимум — это как бы вершина горы, а условный — это самая высокая точка горной тропы, проекция которой на пло­скость х, у имеет уравнение (32).

Если из уравнения связи (32) можно выразить у через х, то этот результат можно подставить в выражение для z

*=/[*, у(х)] (33)

и получить, таким образом, z как функцию одного независимого переменного. Так как условия больше нет, оно учтено подстановкой у — у(х), то задача об отыскании экстремума z становится задачей на безусловный экстремум. Аналогичный результат получится, если

t~ "~

уравнение (32) можно разрешить относительно х или если уравне­ние линии (32) можно представить в параметрическом виде.

Однако такое разрешение уравнения (32) не всегда возможно и целесо­образно. Тогда можно рассуждать так. Уравнение связи (32) определяет принципиально некоторую зависимость у = у(х), хотя бы нам явно и не известную. Таким образом, z является сложной функцией (33) независимой переменной х, и необходимое условие экстремума дает по формуле производ­ной сложной функции

Здесь -Л означает производную неявной функции у (х), определенной из усло­вия (32). Значит (см. п. IX. 13),

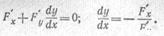
• и Подставляя это выражение в (34), видим, что в точке условного экстремума

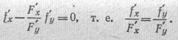
Обозначим значение последнего отношения в рассматриваемой точке через — К ( — взят для удобства, само Я может иметь любой знак). Тогда получим в точке условного экстремума

т. е.

Обозначим

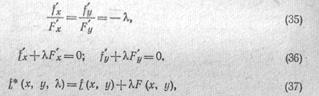
где X—неизвестный параметр, называемый множителем Лагранжа, который разработал данный метод. Тогда уравнения (36) можно записать в виде

£' = °: '# = 0. (38)

Таким образом, получаются такие же уравнения, как и в случае безусловного экстремума [см. уравнении (19)], однако они составляются не для самой функции /, а для измененной функции /*, определенной по формуле (37). Уравнения (38) имеете с уравнением связи (32) образуют систему трех урав­нений с тремя неизвестными х, у, К; из этих уравнений и находятся возмож­ные точки условного экстремума. Полученные условия являются только не­обходимыми; достаточные признаки условного экстремума можно аналогичным образом вывести из достаточных признаков безусловного экстремума (для чего, например, подсчитать d^z/dx*), но мы этого делать здесь не будем.

Множитель Лагранжа К имеет простой смысл. Для выяснения его обозна­чим координаты точки условного экстремума и само экстремальное значение соответственно через х, у и z. До сих пор мы считали h зафиксированным, но если_менять h, то эти три величины будут зависеть от Л. Так как •2>)=И*СО, у(Ц), то

С другой стороны, в силу (32)

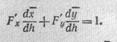
dz

Из (39), (35) и (40) легко получаем, что -jr =^-К. Итак, множитель X,

ah

с точностью до знака, равен скорости изменения экстремального значения z при изменении параметра h в условии.

Для функций любого числа переменных и для любого числа связей исследование условного экстремума проводится аналогично. (Напомним, что согласно п. Х.2 число связей должно быть меньше числа переменных.)

Например, если ищется экстремум функции I (х, у, г, и, v) при условиях

F_l(x, у, г, и, о) = 0, F_z(x, у, г, «, о) = 0, Р₃(х, у, г, «, «) = 0, (41)

то надо поступать так, как если бы надо было искать безусловный экстремум для функции

^-f+Xtfii+Vi+Mv

где xl Я₂, Х₃—неизвестные множители Лагранжа. Требование стационарности для I* дает

^'=°: /;' = °: ^=0; /:' = 0; £'-0.

что вместе с (41) дает 5 + 3 уравнений с 5 + 3 неизвестными х, у, z, и, v, Xj,?i_a> К₃.

Решение задачи на условный экстремум лежит в основе одного из рас­пространенных методов численного нахождения безусловных экстремумов, именно, метода наискорейшего спуска. Мы опишем один из вариантов этого метода на примере функции двух переменных, хотя в принципе он применим для любого числа переменных. Пусть требуется найти точку минимума функ­ции f (х, у). Оказывается, что для сколько-нибудь сложной функции f решить систему уравнений (19) довольно трудно, да к тому же при этом затрачи­вается лишняя работа на отыскание стационарных точек, не являющихся точками минимума. Поэтому можно применить следующий итерационный метод. Начинаем с какого-либо нулевого приближения М_й(х_й\ у₀). В этой точке функция убывает быстрее всего по направлению —grad f = = — fx(*o.?/o) I— fy(x<,, (/o)J (^см- п. 1). Через точку УИ„ проводим луч в этом направлении, т. е. рассматриваем значение f(x₉ — f'_x<jt, y_a — f'ytt) как функцию от t > 0 и находим значение t, при котором эта функция одной переменной имеет минимум. Это значение определяет точку mi(xi, г/j), через которую проводим луч в направлении —(grad {)м^ ищем на нем точку условного минимума / и т. д. Во многих случаях после нескольких шагов мы получаем искомую точку безусловного минимума с хорошей точностью. (Продумайте геометрический смысл этого метода на плоскости х, у с нане­сенными линиями уровня функции f.) Подобные методы нахождения экстре­мумов без обращения к необходимым условиям называются прямыми ме­тодами.

П. Экстремум с ограничениями. На независимые переменные могут быть наложены также одно или несколько соотношений, имеющих вид неравенств; такие соотношения называются ограниче­ниями или высвобождающими связями. Пусть, например, ищется экстремум функции f(x, у), причем независимые переменные свя­заны ограничением F (х, у) ^ 0, определяющим в плоскости х, у

некоторую область (S) с границей (L) (рис. 241), на которой ^=0. Функция / может иметь как внутренние экстремумы, достигающиеся внутри (S), так и граничные экстремумы, достигающиеся на (Z.). Для нахождения первых можно воспользоваться условиями стацио­нарности (19); однако для граничных экстремумов эти условия не действуют. Для нахождения граничных экстремумов можно заметить,

что если в некоторой точке М (рис. 241) функция / имеет экстремум, например мини­мум, то значение f(M) меньше всех значе­ний / на (L) вблизи М. Поэтому в точ­ке М одновременно достигается минимум / при условии F=Q, а такие точки можно разыскать по методу п. 10.

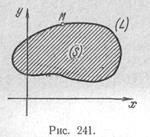
Полученные результаты можно применить к нахождению наибольшего и наименьшего значений функции нескольких переменных. Например, пусть функция z = f(x, у) рас-

сматривается в области, изображенной на рис. 242, причем предпо­ложим, что ни функция, ни ее производные не имеют в этой области разрывов. Если точка, в которой функция принимает наибольшее значение, находится внутри области, то в этой точке будет без-

условный максимум функции. Если эта точка находится на контуре, но не в вершинах А, В, С, то в ней будет условный максимум, причем за усло­вие (32) нужно взять уравнение соот­ветствующей дуги контура. Наконец, наибольшее значение может дости­гаться в вершинах А, В или С.

Таким образом, для отыскания этого значения надо найти все точки без­условного максимума внутри области и все точки условного максимума (или даже все точки возможного условного экстремума, если заранее трудно ска­зать, какие именно из этих точек будут

точками максимума) на контуре и сравнить значения функции / во всех этих точках и в точках А, В и С. Наибольшее из этих зна­чений (наибольший максимум) и даст наибольшее значение функции. Аналогично ищется наименьшее значение функции; как и в п. IV. 19, удобно искать наибольшее и наименьшее значения одновременно.

Если область содержит точки разрыва производных первого порядка, то значение функции в таких точках должно быть «принято к сравнению», так как может оказаться, что наибольшее значение функции достигается именно там. Если имеются точки разрыва функции, то надо дополнительно исследовать пре­дельные значения функции при приближении к таким точкам. Если имеются линии разрыва функции или ее производных первого порядка, то надо исследо-

вать значения функции вдоль таких линий, что приводит к задаче об условном экстремуме. Наконец, если область, на которой рассматривается функция, простирается п бесконечность, то надо дополнительно исследовать предельные значения функции, когда точка в плоскости аргументов удаляется в беско­нечность.

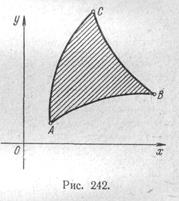
Подобным образом рассматриваются функции большего числа переменных. Но при этом надо иметь в виду, что если, например, функция u = f(x, у, z) рассматривается в области, изображенной на рис. 243, то надо искать без­условные максимумы внутри «кривого тетраэдра», условные максимумы с одним условием на его «гранях» (при этом условием

служит уравнение соответствующей грани) и условные максимумы с двумя условиями на «ребрах», при этом условиями служат уравнения ребер, если их записать в форме (Х.2). Подобным образом поверхности раз­рыва приводят к исследованию условного максимума с одним условием, а линии раз­рыва—к условному максимуму с двумя условиями.

Если применяется итерационный метод типа метода наискорейшего спуска, описан­ного в п. 10, то при наличии нескольких максимумов мы можем прийти не к наиболь­шему. Здесь полезно провести метод не­сколько раз, начиная от различных, выби­раемых наугад, нулевых приближений.

После таких повторных вычислений и сравнения результатов возможно уве­личить максимум, полученный при первом вычислении, а во многих задачах получить и наибольший максимум.

12. Численное решение систем уравнений. Рассмотрим в заключение не­которые методы численного решения системы двух уравнений с двумя неиз­вестными; случай системы п уравнений с п неизвестными рассматривается аналогично.

Метод итераций имеет тот же вид, что в пп. V.3 и VI.5. Для его при­менения заданная система записываете» и виде

Затем выбирается некоторое нулевое приближение х = х₀, у — у^ Последую­щие приближения строятся по формулам

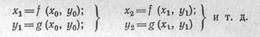
Если процесс сходится, то в пределе получится решение системы (42); сходимость процесса тем лучше, чем медленнее меняются функции / и g при изменении их аргументов, т. е. чем меньше абсолютная величина производных от этих функций.

Иногда некоторое ускорение сходимости удается получить, если на каждом итерационном шаге использовать результаты, полученные уже на этом шаге, т. с. вычислять так (это метод Зайделя): % = / (х_а, у₀), yi = g(x_l,y_a),

*г = /(*i. </i). yt = 8(x* </i) и т. д.

Метод Ньютона (см. п. V.2) состоит в замене заданных функции линей­ными на основе значений этих функций и их производных при значениях аргументов, приближенно равных искомым решениям. Пусть мы решаем систему

уравнений

отправляясь от некоторого нулевого приближения х = х₀,,«/ = </о [^ег° можно найти из физического смысла системы или из ориентировочного наброска линий (43) на плоскости х, у и т. п.] к искомому решению. Применяя раз­ложение (17) функций Р и Q по степеням h — x — х„ и & = {/— у_а и отбрасывая члены высшего порядка_ малости, получим систему уравнений:

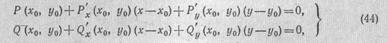
приближенно заменяющую систему (43). Решая систему (44), которая пред­ставляет собой систему линейных уравнений, получаем значения первого приближения x = x_lt у = у\. Второе приближение находится из системы (44), если в ней х_а, у₀ заменить на х_г, r/j и т. д. Связь между га-м и (п-{-\)-м приближениями имеет вид

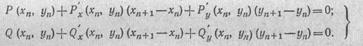
Если процесс сходится, то в пределе при я -> оо в каждом из этих ра­венств два последних слагаемых отпадают, т. е. получается решение системы (43). Можно проверить, что сходимость приближений имеет место, если нуле­вое приближение лежит в достаточной близости от искомого решения и якобиан (см. п. IX. 13)

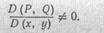
[Чем является этот якобиан для системы (44)?]

Можно воспользоваться также тем, что решение системы (43) одновременно реализует минимум функции V(х, у) = [Р(х, y)]² + [Q(x, у)]² (почему?); впро­чем, иногда перед квадратами ставятся положительные коэффициенты, чтобы в определенном смысле уравнять «значимость» обоих уравнений (43). После этого точка минимума функции V ищется по одному из прямых методов, о которых говорилось в пп. 10 и 11. (Конечно, применять необходимые условия (19) нельзя, так как мы придем опять к системе (43).) Если соответствующее минимальное значение равно нулю, то точка минимума и даст решение системы (43).

Дата добавления: 2015-08-27