Формула Тейлора для функции нескольких переменных.

Рассмотрим для определенности функцию f(x, у) двух переменных,

хотя аналогичные результаты справедлииы для любого числа переменных. Оказывает­ся, что формула (IV.62) без какого-либо изменения остается справедливой и для такой функции /.

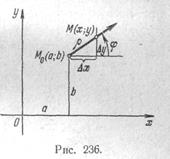
Для доказательства выберем произволь­ное направление, выходящее из точки (а; Ь) в плоскости аргументов и указанное на рис. 236 стрелкой. Вдоль этого направления функция fi зависит от одного аргумента р, т. е. 1(х, у)-=1* ([>). К функции I* можно применить формулу (IV. 62). При этом Д/* = Д^ но при выяснении связи между дифферен-

MU \Ц)П Dm H^llCtlnn *-D«Jn mc/JVAJ дп^р^*- JJV, 11-

циалами функций f* и | надо учесть следующее. Так как (рис. 236)

л: = а + рсо5ф; (/ = Ь + рб!пф (а, Ь, ф = const), (16)

то

f*(9) = f.(x, (/) = /: (я+ р cos ф, Ь + рзтф).

Таким образом, если при составлении df, d²f,... переменные хну счи­таются независимыми, то при составлении df*, d^ff,... они считаются зави­сящими от р. Как известно (см. пп. IX.12 и IX.16), для дифференциала пер­вого порядка это несущественно, т. е. df* = df, но для последующих диф­ференциалов это, вообще говоря, существенно. Однако в рассматриваемом случае из формул (16) видим, что

d?x=t<Px=...=Q; d²j/ = d³//=...=0.

Поэтому из формул (IX.23) и (IX.24) следует, что d²j_j* = d²f, и аналогично d'if* = d³f, и т. д.

Таким образом, из формулы (IV.62) для функции /* автоматически выте­кает справедливость этой же формулы для функции £ (х, у).

В применениях эту формулу обычно обрывают, оставляя лишь один или два члена. Тогда получается (см. п. IX. 16)

/(e + A,* + *)=/(e,*)+/«(e, b)R+/_v(a, b}k + •{-члены не менее второго порядка малости (по сравнению с h и k);

(17) f(a + h,b + k)=*f(a,b)+f'_x(a_t b)h + /_a(a, b)k +

+ -5-[/«(в, Ь) h* + 2/_w (a, b) hk +/;_v (a, b) k*} -f

-f-члены не менее третьего порядка малости. (18)

Как и для функций одного переменного, формулами (17) и (18) можно пользоваться, если |А| и \k\ малы, в противном случае фор­мулы могут привести к ошибочным выводам. Во всех случаях при-

j

менения формулы Тейлора, конечно, предполагается, что рассматриваемые производные существуют и конечны. 7. Экстремум. Как и в п. 6, мы будем для простоты считать, что рас­сматривается функция двух переменных z—f(x, у). Определение экстремума дается аналогично случаю функций одного переменного (п. IV. 18). Напри­мер, мы говорим, что функция имеет максимум «в точке» (т. е. при значе­ниях) х = х₀, у — у₀, если значение f(^xoi Уо} больше всех «соседних» зна­чений функции /, т. е. значений/(#, у)

чении функции /, т. е. значении f(X, у) при х, достаточно близких к х₀, и у, достаточно близких к у₀.

В этом пункте мы будем рассматривать только внутренние экст­ремумы, т. е. точки экстремума, лежащие внутри области опреде­ления функции /, причем будем считать, что сама функция /и ее част­ные производные не имеют разрывов. Примерный инд семейства линий уровня (см. п. IX.1) около точки экстремума показан на рис. 237.

Легко вывести необходимое условие экстремума: если зафикси­ровать у — у₀ и изменять х, т. е. на рис. 237 следовать вдоль пря­мой //, то функция / будет иметь при х = х₀ экстремум. Но при таком рассмотрении функция f=f(x,y_u) будет зависеть только от х и потому согласно п. IV. 18 /; (х₀, у₀) = 0; производная частная, так как она берется при фиксированном у. Аналогично рассматри­вается случай следования по прямой х = х₀, и мы получаем необ­ходимые условия экстремума:

f'_x(x_u, </o) = 0, /J(*₀, г/₀) = 0 (19)

(для функций большего числа переменных надо приравнять нулю все частные производные первого порядка). Точка (в плоскости аргу-

ментов), в которой выполняются условия (19), называется стацио­нарной точкой функции /. Таким образом, в предположениях, ука­занных в предыдущем абзаце, все точки, экстремума функции f явля­ются ее стационарными точками.

Обратно, пусть у функции f(x, у) найдена какая-либо стацио­нарная точка (х₀; у₀); будет ли она точкой экстремума? Если в какой-либо области стационарная точка имеется только одна, а существование там экстремума вытекает из физических или каких-либо иных соображений, то ясно, что ответ утвердительный. В дру­гих случаях приходится обращаться к достаточным условиям экстре­мума, к которым мы и переходим.

Как известно из п. IV. 18, для- функции f(x) одного переменного необходимое условие /' (х₀) — О экстремума является «почти доста­точным»: например, если f"(x₀)=^0, то в точке х = х₀ обязательно будет экстремум. Можно было бы ожидать, что и для функции двух переменных при выполнении условия (19) экстремум в точке (Х₀; у₀) обязательно будет, если в ней частные производные второго порядка отличны от нуля. Замечательно, что это, вообще говоря, не обяза­тельно: так, функции нескольких переменных доставляют случаи прин­ципиально нового типа.

Так, «график» функции z=f(x, y) = x^a-}-y^z показан на рис. 220. Условия (19) дают единственную стационарную точку (0; 0). Ясно, что в ней будет минимум, так как г (О, 0) = 0, а в остальных точ­ках 2>0. Принципиально иной случай будет для функции z = = — х^а-\-у*, «график» которой показан на рис. 221. И здесь един­ственной стационарной точкой служит начало координат. При лг=0 получаем z=--y*, т. е. от начала координат вдоль оси у функция в обе стороны возрастает, а и самом начале имеет минимум. Если же у = 0, то г= —л², т. е. вдоль оси х функция в обе стороны убы­вает, а в самом начале имеет максимум. Если рассматривать другие прямые, проходящие через начале координат, то вдоль одних из них функция имеет в начале максимум, а вдоль других — минимум. Такой случай называется минимакс, и здесь экстремума в начале коорди­нат не будет, хотя необходимые условия (19) выполняются и част­ные производные второго порядка не все равны нулю.

Перейдем от примеров к функциям общего вида. Допустим, что в некоторой точке (х_а; у₀) выполняются условия (19), и мы хотим выяснить, действительно ли функция / имеет в этой точке экстре­мум. Тогда следует воспользоваться формулой Тейлора (18), поло­жив в ней а = х_в, Ь = у₀; получим

A/ = /(*o + A, yo + k) — f(x₀, у₀) =

= у [/**(*„, 0о)** + 2/зд(*в, y₀)hk+f"_yu(x₀, t/o) ft²]+

-f- члены не менее третьего порядка малости, члены первого порядка отсутствуют из-за условий стационарности

-......----------..,и...,лл игипОПиДПМЛ [ГЛ. XII

(19). Так как при малых \h\, \k\ члены третьего порядка значитель­но меньше членов второго порядка, то знак всей правой части определяется знаком суммы членов второго порядка малости, т. е. знаком квадратичной формы

P(h, k) =/_хх (х₀, г/₀) А² + 2А„ (х₀, _Уо) hk +/;, (х₀, у₀) k\ (20) мы не пишем коэффициент -=-, так как он для выяснения знака не­существен. Таким образом, если, эта сумма положительна при всех h, k (конечно, кроме значений А = & = 0, когда она равна нулю), то в точке (х₀; у₀) будет минимум, так как тогда при достаточно малых |й|, |й| будет А/>0, т. е. f(x₀ + fi, y₀ + k)>f(x₀, y_a). Если эта сумма отрицательна, то в точке (х₀; у₀) будет максимум. Если эта сумма может принимать значения обоих знаков, то в точке (Х₀; у₀) будет минимакс и экстремума не будет. Единственный случай, когда по сумме членов второго порядка нельзя судить о наличии экстремума, тот, когда эта сумма знака менять не может, но может обращаться в нуль (в частности, если она полностью отсутствует). Тогда формулу Тейлора надо продолжить, выписав члены третьего порядка, и провести аналогичное исследование суммы этих членов при тех значениях A, k, при которых сумма членов второго порядка равна нулю. Мы не будем здесь этого делать.

Полученные выводы формулируются совершенно аналогично для функций любого числа переменных. Однако для функций двух пере­менных легко пойти дальше и получить достаточные признаки экстре­мума, выраженные непосредственно через значения производных вто­рого порядка в точке (д;₀; у₀). Для этого вынесем в правой части

k (20) h² за скобки и обозначим ~r = t- Тогда получим

Р(Ь, ^ = [(/«)„ + 2 (f"_xy)₀ t + (/;,)„ /²] А² (21)

(индекс «нуль» указывает на то, что значения производных берутся в рассматриваемой стационарной точке (х₀; у₀)). Из элементарной алгебры известно, что если дискриминант

(A»)J-(A*)o(/w)o>0, (22)

то многочлен относительно t, стоящий в квадратных скобках, имеет два вещественных нуля, при переходе через которые он меняет знак. Значит, это — случаи минимакса. Если же

(A»);-(/I*)o(/w)o<°.

то указанный многочлен имеет мнимые нули и потому знака не ме­няет (почему?). Значит, это — случай экстремума. Чтобы узнать, какой именно знак имеет правая часть (21), положим / = 0. Мы ви­дим, что если

(/«)?-(Л*)о(Л*)о<°, (А*)о>0, (23)

то правая часть (21) положительна при всех t и потому в силу предыдущего абзаца функция / имеет в точке (х_а', у₀) минимум. Если же

(/«„)! — (/«)о(ЛЛ<°. </«)о<°. (²⁴>

то функция / имеет максимум. Наконец, если

(«-(/;л(/шЛ>=°. (25)

то многочлен (21) имеет двойной корень, а потому знака не меняет, но может обратиться в нуль; это — неопределенный случай.

Условие положительности квадратичной формы (20) можно вывести также из общей теории квадратичных форм (п. XI. 11). Согласно этой теории после некоторого поворота осей координат форма (20) приобретает «диагональный вид»

P = A,iA'⁸ + X_afe'², (26)

где К₁ и К₂ —корни характеристического уравнения

здесь h' и k' —приращения координат после поворота. Из (27) следует (про­верьте!), что

*л=(Оо (4)о-(4)о- ^-гЛ=(4)»+(О»

Из этих равенств легко вывести, что мы предоставляем читателю, что в слу­чаях (22) —(25) будет соответственно XjX₂ < 0; Х_х > О, Х₃ > 0; Xj < 0, \₂ < 0; ^^2 = 0. Отсюда с помощью равенства (26) получаем те же выводы, что в предыдущем абзаце.

Для функции /;(*!, лг_а,..., х_п) от любого числа п аргументов в стацио­нарной точке взамен (20) надо рассмотреть квадратичную форму

S (С>^Л^ ⁽²⁸⁾

I. /= 1 а взамен (27) — уравнение

det(A-M) = 0, где А = ((£„,)„)„„. (29)

Если все корни уравнения (29) положительны, то форма (28) принимает толь­ко положительные значения; такая форма называется положительно опреде­ленной. В этом случае функция /; имеет в рассматриваемой стационарной точке минимум. Если все корни уравнения (29) отрицательны, то форма (28) отрицательно определенная и функция I имеет максимум. Если же уравне­ние (29) имеет корни обоих знаков, то функция I имеет минимакс.

8. Метод наименьших квадратов. В качестве примера на экстре­мум функции двух переменных рассмотрим метод наименьших квад­ратов при построении эмпирических формул. Он применяется, если точность грубого метода, указанного в п. 1.30, нас не устраивает, а также при автоматизации вычислений. Мы остановимся здесь только на выборе линейной зависимости в случае одной независимой переменной. При этом рассуждают так (для других зависимостей

Дата добавления: 2015-08-27