
Читайте также:
|
Цель работы
Изучить теоретические основы целочисленного линейного программирования, общую схему метода ветвей и границ, а также возможности его применения к решению целочисленных задач, научиться решать целочисленные задачи с помощью метода ветвей и границ.
Метод ветвей и границ решения задач
целочисленного линейного программирования
2.1. Постановка задачи целочисленного линейного программирования
Задача линейного программирования, переменные которой могут принимать только целые значения, является задачей целочисленного линейного программирования:




где 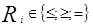 ; xj - переменные, aij, bi, cj - константы.
; xj - переменные, aij, bi, cj - константы.
Записанная в таком виде задача представляет собой полностью целочисленную задачу. Существуют, кроме того, частично целочисленные задачи, в которых ограничения целочисленности наложены только на часть переменных, а остальные переменные могут быть как целыми, так и дробными.
Примером целочисленной задачи в экономике может служить задача производственного планирования, в которой в качестве продукции выступают корабли, дома, вагоны и т.п. предметы, выпуск которых нельзя измерить в непрерывной шкале. Часто переменные в экономико-математических моделях измеряются в количестве человек, которое также не может быть дробным.
На первый взгляд, тривиальным подходом к решению такой задачи является решение задачи линейного программирования без ограничений целочисленности и последующее округление полученного решения до целых. Однако в общем случае такой подход неверен, так как он может привести к одной из двух ошибок. Во-первых, при округлении возможен выход за пределы ОДП, т.е. полученное решение не будет удовлетворять ограничениям. Во-вторых, даже оставшись в пределах ОДП, можно в результате получить неоптимальное решение.
Поэтому округление допустимо использовать лишь в тех случаях, когда по своему экономическому смыслу целочисленные переменные не представляют особо ценные объекты, либо в модели рассматривается очень большое количество таких объектов; т.е. нет необходимости получить точное решение. В противном случае задача должна ставиться, как целочисленная, и к ее решению необходимо применить специфические методы, которые обычно относятся к одной из трех групп:
1. Метод ветвей и границ.
2. Методы отсечения.
3. Методы динамического программирования.
Здесь будет рассмотрен метод из первой группы.
2.2. Метод ветвей и границ. Общая схема
Метод ветвей и границ представляет собой комбинаторный метод, т.е. упорядоченный перебор вариантов и рассмотрение лишь тех из них, которые по некоторым признакам оказываются перспективными. Он имеет достаточно широкую сферу применения, поэтому рассмотрим его общую схему.
Пусть существует некоторая функция f(X), экстремум которой (например, максимум) необходимо найти при некоторой системе ограничений.
Этой системой определяется ОДП задачи - обозначим ее G. Пусть некоторым способом мы можем определить верхнюю границу функции на этой области  0, т.е.
0, т.е.  0
0  f(X), X
f(X), X  G.
G.
Затем проверяют, не существует ли какой-нибудь очевидный способ нахождения точки X0, для которой f(X0)=  0. Если он есть, то искомый максимум найден.
0. Если он есть, то искомый максимум найден.
Если такого способа нет, то множество G разбивают на подмножества G1 и G2 и для каждого из них находят верхнюю границу  1 и
1 и  2 (при этом
2 (при этом  0
0 
 1 и
1 и  0
0 
 2). Далее оптимальный план ищут в наиболее перспективном множестве, т.е. в том, которому соответствует наибольшая оценка.
2). Далее оптимальный план ищут в наиболее перспективном множестве, т.е. в том, которому соответствует наибольшая оценка.
 |
Этот процесс может быть изображен в виде дерева (рис.1). На каждом шаге процесса делается попытка найти точку Х в соответствующем подмножестве, на которой реализуется его верхняя граница. Если попытка не удается, то ветвление продолжают, рассматривая каждый раз наиболее перспективное подмножество (для его выбора сравнивают оценки вершин дерева, из которых нет выходов).
Если попытка найти Х: f(X) =  k удалась, то это будет оптимальный план для всего исходного множества G (поскольку для остальных подмножеств верхние границы заведомо меньше).
k удалась, то это будет оптимальный план для всего исходного множества G (поскольку для остальных подмножеств верхние границы заведомо меньше).
При решении задачи на минимум схема та же, но рассматриваются вершины с наименьшей оценкой.
Этот метод всегда сходится, если мы имеем дело с ограниченной дискретной областью.
Чтобы конкретизировать метод ветвей и границ, необходимо установить:
1) алгоритм поиска границ  ;
;
2) алгоритм разбиения множества на части;
3) алгоритм поиска Х, реализующего границу  ;
;
4) установить сходимость.
2.3. Применение метода ветвей и границ
к решению задач линейного целочисленного программирования
Рассмотрим задачу ЦЛП в матричной форме записи. Обозначим ОДП этой задачи D, а ОДП ЗЛП без ограничений целочисленности - G. Точно так же обозначим соответствующие системы ограничений, а сами задачи будем называть D-задача и G-задача.
max CX

D представляет собой часть G. G будем рассматривать в качестве исходного множества (рис.2).

Решим вначале G-задачу. Пусть при решении этой задачи получен оптимальный план ХG. Значение целевой функции на нем zG - оптимум G-задачи - будем использовать в качестве границы  . В самом деле,
. В самом деле,
zG  СХ
СХ 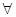 Х
Х  G
G
zG  СХ
СХ 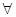 Х
Х  D
D
Если план ХG целочисленный, то решение задачи окончено. Таким образом, мы ответили на первый и третий вопросы, конкретизирующие метод ветвей и границ.
Предположим, что хотя бы одна компонента ХG нецелочисленна: хGi 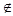 Z.
Z.
Целой частью числа называют наибольшее целое число, меньшее или равное данному.
Обозначим целую часть числа хGi [хGi].
Конкретизируем второй вопрос.
Разобьем D на D1 и D2 следующим образом:
D1={X  D: хi
D: хi  [хGi]}
[хGi]}
D2={X  D: хi
D: хi  [хGi] + 1}
[хGi] + 1}
(т.е. к одному множеству отнесли все допустимые планы, у которых i-я компонента не больше целой части хGi, а к другому - у которых не меньше следующего целого числа)
Разбивая D, мы одновременно разбиваем и G (рис.3).
Это разбиение обладает следующими свойствами:
 G1
G1  G2
G2  G (объединение этих множеств содержится в G, но не равно ему)
G (объединение этих множеств содержится в G, но не равно ему)
D1  D2 = D (в устраненном «коридоре» нет ни одной точки с целочисленными координатами)
D2 = D (в устраненном «коридоре» нет ни одной точки с целочисленными координатами)

При этом устраняется и план ХG.
Далее решение задачи продолжается для каждого из подмножеств G1 и G2.
Сходимость алгоритма основана на том, что в ограниченной ОДП множество дискретных точек конечно.
Следует отметить, что метод ветвей и границ легко обобщается и на частично целочисленные задачи (в качестве переменной, по которой разбивается множество, выбирают одну из тех, на которые наложены ограничения целочисленности).
2.4. Пример решения задачи целочисленного линейного программирования методом ветвей и границ
Например,
max 2х1 + х2
5х1 + 2х2  10
10
3х1 + 8х2  13
13
х1,2  0
0
х1,2  Z
Z
Вначале решим эту задачу графически без ограничений целочисленности (рис.4).

Координаты точки оптимума можно найти, решив систему уравнений:
5х1 + 2х2 = 10 х1=27/17
3х1 + 8х2 = 13 х2=35/34
ХG = (27/17;35/34), zG=143/34
Начнем строить дерево, первая вершина которого будет соответствовать всей ОДП нецелочисленной задачи (G), а ее оценка будет равна zG (рис.5).

Полученный план не является целочисленным, поэтому возьмем его произвольную нецелочисленную компоненту, например, первую (х1 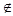 Z; [х1] = [27/17] = 1) и разобьем ОДП на две части следующим образом:
Z; [х1] = [27/17] = 1) и разобьем ОДП на две части следующим образом:
G1={X  G: х1
G: х1  1}
1}
G2={X  G: х1
G: х1  2}
2}
Изобразим это графически (рис.6).

Из рис.7 видно, что G2 представляет собой одну точку ХG2=(2;0), следовательно, на этом множестве оптимум задачи равен 4 ( 2=4).
2=4).
План ХG2 является целочисленным, следовательно, решение целочисленной задачи уже, возможно, найдено. Однако, следует еще найти оценку множества G1. Она может оказаться не менее 4 (но обязательно не более 143/34). Если это так, то нужно проверить, не является ли целочисленным решение задачи на G1. Если оно целое, то является решением задачи, а если нет, то процесс решения необходимо продолжить, разбивая G1.
На G1 точку оптимума можно найти, решив систему уравнений:
х1 = 1 х1=1
3х1 + 8х2 = 13 х2=5/4
ХG1 = (1; 5/4), zG=13/4
Оценка меньше 4, следовательно, решением задачи является Х*=ХG2=(2;0),z*=4.
2.5. Решение задачи целочисленного линейного программирования методом ветвей и границ с помощью пакета QSB
Соответствующая программа запускается файлом intlprog.exe. Она решает как частично, так и полностью целочисленные задачи линейного программирования с числом переменных и ограничений до 20, используя метод ветвей и границ. В том числе решаются и задачи с булевыми переменными. По умолчанию все переменные неотрицательны. Программа позволяет ввести целочисленные границы для переменных, не включая их в общее число ограничений. По умолчанию нижняя граница 0, а верхняя 32000. Если необходимо установить нецелочисленные границы, их вводят, как обычные ограничения.
Если в задача имеется несколько оптимальных планов, из них находится только один. Информация о наличии множественного решения не выводится.
Режим 2 (ввод новой задачи) включает три этапа. На первом этапе осуществляют ввод информации о размерности задачи, направлении экстремизации и именах переменных (по умолчанию X1,X2,...,Xn).
На втором этапе необходимо определить, являются ли все переменные целочисленными, являются ли все переменные булевыми, и будут ли вводиться границы для переменных. При ответе «нет» на первый вопрос или «да» на третий, выводится таблица:

Установив I в столбце «Предел», на переменную накладывают ограничение целочисленности. В противном случае (С) - переменная может принимать и нецелые значения.
Значения границ округляются до целых. Если нижняя больше верхней, выдается сообщение об ошибке.
На третьем этапе вводятся коэффициенты при переменных и знаки в ограничениях.
В меню решений имеется возможность исправить целочисленную погрешность (по умолчанию она 0,001).
Решение задачи методом ветвей и границ не сопровождается графической иллюстрацией (изображением дерева) в программе, но здесь она приводится для пояснения алгоритма (рис.7).
Алгоритм метода ветвей и границ, реализованный в данной программе, несколько отличается от рассмотренного выше в методических указаниях и является менее эффективным в том смысле, что может потребовать большего числа итераций. Тем не менее, его полезно рассмотреть, чтобы наглядно проиллюстрировать разницу в подходах. Кроме того, во многих учебных пособиях применение метода ветвей и границ рассматривается именно на примере данной его модификации.
Основное различие заключается в том, что здесь на каждом этапе не выбирается наиболее «перспективное» подмножество. После того, как очередное подмножество разбито на две части, не подсчитывают сразу оценку обеих частей, а вместо этого каждая ветвь дерева последовательно рассматривается до конца. Исходная ОДП разбивается на подмножества по первой нецелочисленной переменной в оптимальном плане нецелочисленной задачи. Затем рассматривают ту вершину, которой соответствует знак  , разбивают соответствующее подмножество так же, как и исходную ОДП, снова рассматривают ту вершину, которой соответствует знак
, разбивают соответствующее подмножество так же, как и исходную ОДП, снова рассматривают ту вершину, которой соответствует знак  , и т.д. до тех пор, пока не будет получен целочисленный план, или задача окажется неразрешимой. Только после этого возвращаются к рассмотрению вершин, которым соответствовал знак
, и т.д. до тех пор, пока не будет получен целочисленный план, или задача окажется неразрешимой. Только после этого возвращаются к рассмотрению вершин, которым соответствовал знак  .
.
При этом на каждой итерации выводится информация о текущих целочисленных границах (определяющих рассматриваемое подмножество), оптимальном плане нецелочисленной задачи, о том, является ли он целочисленным, о значении целевой функции (ЦФ) на нем и о величинах ZL или ZU. Для задачи на максимум выводится значение нижней границы ZL, а на минимум верхней ZU. До тех пор, пока не найдено какое-нибудь целое решение, ZL =-1*1020, а ZU = 1*1020.
После нахождения целочисленного плана нельзя сразу судить о том, является ли он оптимальным, так как рассматривались не наиболее перспективные вершины. Но можно в уверенностью утверждать, что искомый максимум не меньше (а минимум не больше) значения целевой функции на целочисленном плане. Поэтому значения границ ZL и ZU изменяются (если только ранее не был найден целочисленный план с не меньшим (не большим) значением целевой функции).
Ветви с оценкой, меньшей ZL или большей ZU, не рассматриваются. План, соответствующий границе, запоминается. После того, как рассмотрены или исключены из рассмотрения все подмножества, этот план можно считать оптимальным.
Поясним это на примере (рис.7):
max 3х1 + 2х2
7х1 + 5х2  35
35
9х1 + 4х2  36
36
х1,2  0
0
х1,2  Z
Z
На первой итерации найдено нецелочисленное решение Х=(2,353; 3,706). Вся ОДП (множество G) разбивается на два подмножества - G1 и G2 следующим образом:
G1={X  G: х1
G: х1  3}
3}
G2={X  G: х1
G: х1  2}.
2}.
На второй итерации решают задачу на подмножестве G1. Полученное решение также нецелочисленно. Далее, вместо того, чтобы рассмотреть подмножество G2, продолжают рассматривать G1. В соответствующем плане выбирают первую по счету нецелочисленную компоненту (это х2) и разбивают G1 на G3 и G4. На третьей итерации рассматривают G3 - на этом подмножестве допустимых планов нет. Только после этого на четвертой итерации рассматривается вторая ветвь, выходящая из G1 - подмножество G4. Далее аналогично.
На пятой итерации на подмножестве G5 найдено целочисленное решение, которому соответствует значение целевой функции 12. На следующей итерации это значение присваивается величине ZL, которая до этого была равна -1*1020. Соответствующий план запоминается - он может оказаться оптимальным. Но на шестой итерации снова получен целочисленный план, целевая функция на котором равна 13 (больше 12) - ZL снова изменяется, запоминается новый план.
После этого, на седьмой итерации, переходят к рассмотрению подмножества G2, которое разбивают на G7 и G8.
На тринадцатой итерации (подмножество G14) снова найдено целочисленное решение Х=(0; 7), целевая функция на нем равна 14. Снова изменяется ZL и запоминается соответствующий план.
План, найденный на четырнадцатой итерации, также является целочисленным, но его не запоминают, так как 13<14 (ZL=14). План, найденный на пятнадцатой итерации, тоже, к сожалению, не запоминается, так как 14  14, а программа ставит своей целью найти хотя бы одно решение.
14, а программа ставит своей целью найти хотя бы одно решение.
Наличие других оптимальных планов здесь игнорируется.
Таким образом, решение Х=(0; 7) получено за 15 итераций.
Отметим, что если бы использовался более эффективный вариант метода ветвей и границ, схема которого описана в методических указаниях, то после второй итерации произошел бы сразу переход к седьмой. В самом деле, если рассматривать значения целевой функции на соответствующих планах в качестве оценки подмножеств, то оценка G2 выше. Поэтому итерации с 3-ей по 6-ю оказываются лишними, и общее число итераций могло быть равно 11.

Для задачи с булевыми переменными алгоритм метода ветвей и границ будет тот же, но разбиение проводится по первой по счету переменной, значение которой не равно 0 или 1. На одном подмножестве эта переменная приравнивается 1 (эта ветвь рассматривается вначале), а на другом - нулю.
Следует отметить, что для таких задач разработан более эффективный алгоритм решения (так называемый аддитивный), также основанный на методе ветвей и границ. В нем обычно требуется меньшее число итераций, а кроме того, и расчеты на каждой итерации являются менее трудоемкими, не требуют применения симплекс-метода. Но в данном пакете этот алгоритм не реализован, он будет изучен позднее в другой лабораторной работе.
Рассмотрим решение задачи с булевыми переменными в данной программе на следующем примере:
max 4x1 + 2x2 - 5x3 - 2x4 + 3x5
x1 + x2 + x3 + 2x4 + x5  4
4
7x1 + 3x3 - 4x4 + 3x5  8
8
11x1 - 6x2 + 3x4 - 3x5  3
3

Ход решения (7 итераций) проиллюстрирован рисунком 8.
 | |||
|
Возможности корректировки исходных данных в данной программе рекомендуется изучить самостоятельно.
Содержание работы
1. Изучение основных понятий целочисленного линейного программирования и экономической интерпретации задачи.
2. Изучение основ метода ветвей и границ.
3. Решение задач целочисленного линейного программирования методом ветвей и границ.
4. Решение задач целочисленного линейного программирования, в том числе с булевыми переменными, с помощью ППП «Система деловых задач».
Дата добавления: 2015-08-27; просмотров: 201 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Применение метода ветвей и границ к решению задач линейного целочисленного программирования | | | Порядок выполнения работы |