Сложение. Вычитание. Умножение. Деление.

Арифметические операции

Возведение в степень. Извлечение корня.

Сложение является начальным понятием, для которого невозможно дать строгое формальное определение. Тем не менее, чтобы придать этому действию некоторое разумное представление, мы скажем, что сложение – это операция нахождения суммы двух или нескольких чисел, где под суммой понимается общее количество единиц, содержащихся в рассматриваемых числах вместе. Эти числа называются слагаемыми. Например, 11 + 6 = 17. Здесь 11 и 6 – слагаемые, 17 – сумма. Если слагаемые поменять местами, то сумма не изменится: 11 + 6 = 17 и 6 + 11 = 17.

Вычитание является действием, обратным к сложению, так как это операция нахождения одного из слагаемых по сумме и другому слагаемому. Вычесть из одного числа (уменьшаемого) другое (вычитаемое) - значит найти такое третье число (разность), которое при сложении с вычитаемым дает уменьшаемое: 17 – 6 = 11. Здесь 17 – уменьшаемое, 6 – вычитаемое, 11 – разность.

Умножение. Умножить одно число n (множимое) на другое целое число m (множитель) - значит повторить множимое n в качестве слагаемого m раз. Результат умножения называется произведением. Запись операции умножения: n x m или n ∙ m. Например, 12 x 4 = 12 + 12 + 12 + 12 = 48. Таким образом, 12 x 4 = 48 или 12 ∙ 4 = 48. Здесь 12 – множимое, 4 – множитель, 48 – произведение. Если множимое n и множитель m поменять местами, то произведение не изменится. Например, 12 · 4 = 12 + 12 + 12 + 12 = 48 и соответственно, 4 · 12 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 48. Поэтому множимое и множитель часто называются сомножителями.

Деление является действием, обратным к умножению, так как это операция нахождения одного из сомножителей по произведению и другому сомножителю: Разделить одно число (делимое) на другое (делитель) – значит найти такое третье число (частное), которое при умножении на делитель даёт делимое: 48: 4 = 12. Здесь 48 – делимое, 4 – делитель, 12 – частное. Частное от деления одного целого числа на другое целое число может и не быть целым числом. Тогда это частное представляется в виде дроби. Если частное – целое число, то говорят, что эти числа делятся нацело. В противном случае мы выполняем деление с остатком. Пример: 23 не делится на 4, в этом случае мы можем записать: 23 = 5 · 4 + 3. Здесь 3 – остаток.

Возведение в степень. Возвести число (основание степени) в целую степень (показатель степени) – значит повторить его сомножителем столько раз, каков показатель степени. Результат называется степенью. Запись возведения в степень:

3 ⁵ = 3 · 3 · 3 · 3 · 3 = 243.

Здесь 3 – основание степени, 5 – показатель степени, 243 – степень.

Вторая степень любого числа называется квадратом, третья – кубом. Первой степенью любого числа является само это число.

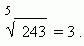Извлечение корня является действием, обратным к возведению в степень, так как это операция нахождения основания степени по степени и её показателю. Извлечь корень n- ой степени (n – показатель корня) из числа a (подкоренное число) – значит найти третье число, n -ая степень которого равна а. Результат называется корнем. Например:

Здесь 243 – подкоренное число, 5 – показатель корня, 3 – корень.

Корень второй степени называется квадратным, корень третьей степени – кубическим. Показатель квадратного корня не записывается:

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня являются попарно взаимно-обратными операциями.

Дроби

Дата добавления: 2015-08-27