Читайте также:
|
Если в полном графе п вершин, то число различных гамильтоновых контуров равно произведению (п -1)(п -2) ∙ … ∙2∙1=(п -1)! Это число очень быстро растет с ростом п. Уже при п = 7 оно равно 720, так что полный перебор всех вариантов даже для графа с семью вершинами отнимет много времени. Метод ветвей и границ позволяет найти гамильтонов контур минимальной длины, избежав полного перебора вариантов. Изложим метод на примере анализа конкретного графа с семью вершинами (табл. 1). В табл. 1 записаны длины дуг графа (времена tij переезда из города i в город j). На главной диагонали вместо нулей стоят бесконечности. Смысл такой замены станет понятен в процессе изложения метода.
Таблица 1
| j i | 
| |||||||
| ∞ | ||||||||
| ∞ | ||||||||
| ∞ | ||||||||
| ∞ | ||||||||
| ∞ | ||||||||
| ∞ | ||||||||
| ∞ |
Табл. 1 назовем матрицей длин дуг.
Приведение матрицы длин.
В любом гамильтоновом контуре в каждую вершину входит ровно одна дуга и ровно одна дуга выходит из каждой вершины. Следовательно, для построения контура по матрице длин нужно взять ровно одно число из каждой строки (выходящая дуга) и ровно одно число из каждого столбца (входящая дуга). Значит, если длины всех дуг некоторой строки (столбца) уменьшить на одно и тоже число, то длина каждого гамильтонова контура уменьшится на это же число. Эта операция называется приведением матрицы по строкам (столбцам). Приведём нашу матрицу по строкам. Вычтем из каждой строки минимальное число (табл. 2).
Минимальные элементы строк табл. 1 записаны в ее крайнем правом столбце
Таблица 2
| j i | |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ | |||||||
|
Приведение матрицы по строкам уменьшило длину каждого из гамильтоновых контуров данного графа на величину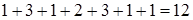 
. При этом в каждой строке матрицы длин появился по крайней мере один 0. Но матрицу можно допривести по столбцам: все длины второго и третьего столбцов больше нуля. Уменьшим на 1 все длины дуг, входящих во вторую вершину и на 4 длины всех дуг, входящих в третью вершину (доприведем матрицу по второму и третьему столбцам).
Результат представлен в табл. 3. Теперь в каждой строке и каждом столбце матрицы длин есть хотя бы один 0 (хотя бы одна дуга нулевой длины).
Длина каждого гамильтонова контура уменьшилась еще на 5 единиц, так что любой контур данного графа имеет длину не менее 12 + 5 = 17. Это число называется нижней границей длин всех гамильтоновых контуров данного графа (напомним, что их всего 720).
Будем выбирать дуги для контура из табл. 3. Если бы нам удалось выбрать 7 дуг длины 0, образующих гамильтонов контур, он заведомо был бы минимальным, длины 17. Не обязательно, что такой контур существует.
Таблица 3
| j i | |||||||
| ¥ | 0(1) | ||||||
| ¥ | 0(1) | ||||||
| ¥ | 0(2) | ||||||
| ¥ | 0(2) | ||||||
| 0(0) | 0(0) | 0(0) | ¥ | ||||
| 0(0) | 0(2) | 0(0) | 0(0) | ¥ | |||
| 0(1) | ¥ |
Процесс построения гамильтонова контура наименьшей длины заключается в следующем.
Ø На каждом шаге рассматривается некоторое множество М гамильтоновых контуров данного графа. Первоначально это множество U всех 
контуров.
Ø Известна нижняя граница r (M) длин всех контуров множества М: длина любого из них не меньше числа r (M).
Ø Множество М разбивается (ветвится) на два непересекающихся подмножества М ′ и М ″ так, что все контуры, принадлежащие множеству М ′, содержат некоторую дугу (u, v) нулевой длины, а все контуры множества М ″ не содержат дуги (u, v).
Ø Дуга (u, v) выбирается так, чтобы нижняя граница r (M″) длин контуров множества М ″ была как можно больше.
Ø После завершения очередного ветвления из всех подмножеств, на которые оказалось разбито множество U всех гамильтоновых контуров данного графа, выбирается множество с наименьшей нижней границей для дальнейшего ветвления.
Ø В конце концов, будет найдено множество М с наименьшей нижней границей, содержащее единственный контур. Он минимален.
Процесс ветвления можно представить ориентированным деревом, которое называется деревом ветвлений. Каждая вершина дерева соответствует одному из множеств М, полученных в процессе ветвления. Корень дерева соответствует множеству U. Над вершиной записывается нижняя граница r(M). Внутри вершины записывается или символ дуги (u, v) – признак того, что все контуры данного множества содержат эту дугу, либо символ 
– признак того, что все контуры данного множества эту дугу не содержат.
Начнем ветвление множества 720 гамильтоновых контуров нашего графа. Просмотрим последовательно все дуги нулевой длины в табл. 3.
Начнем с дуги (1,5). Всякий гамильтонов контур, не содержащий дугу (1,5), должен содержать некоторую другую дугу, выходящую из первой вершины, и какую-то другую дугу, входящую в пятую вершину. После запрета дуги (1,5) в первой строке табл. 3 (строке длин дуг, выходящих из первой вершины), минимальная длина равна 1 (дуга (1,7)). В пятом столбце табл. 3 (столбце длин дуг, входящих в вершину 5) минимальная длина по-прежнему равна 0 (дуга (6,5)). Таким образом, всякий гамильтонов контур, не содержащий дугу (1,5) имеет приведенную длину не меньше 1 (длина 1 получится, если удастся «собрать» этот контур из дуги (1,7) длины 1 и остальных шести дуг длины 0), реальная же длина всякого контура, не содержащего дугу (1,5), не меньше, чем 
.
По-другому: нижняя граница длин циклов, не содержащих дугу (1,5) равна 18. В табл. 3 в клетке (1,5) запишем над нулем (длиной дуги (1,5)) символ (1) – знак того, что запрет дуги (1,5) поднимает нижнюю границу длин контуров на 1. Итак, 1 - это сумма минимальных элементов первой строки и пятого столбца табл. 3, если в ней исключить 0, стоящий в клетке (1, 5). Просмотрим таким же образом все дуги длины 0 в табл. 3. В ней имеются три дуги - (3,7), (4,6), (6,2), запрет которых максимально увеличивает нижнюю границу r – на 2. Выберем для ветвления любую из них, например, (3,7). Дерево ветвлений показано на рис. 4.
Оценим длину циклов, содержащих дугу (3,7). Для чего удалим из матрицы длин строку 3 (удаляются другие дуги, выходящие из вершины 3) и столбец 7 (удаляются другие дуги, входящие в вершину 7) (табл. 4).
Кроме того, всякий гамильтонов контур, содержащий дугу (3,7), не может содержать дугу (7,3), так как эти две дуги образуют мини-контур, охватывающий две вершины (рис. 3). Чтобы запретить дугу (7,3) положим, что ее длина равна 
. Никакой контур конечной длины не будет содержать эту дугу.
В каждой строке и в каждом столбце табл. 4 есть нули. Это означает, что нижняя граница длин циклов, содержащих дугу (3,7) остается равной 17 (рис. 4).
Выберем в табл. 4 дугу нулевой длины, запрещение которой максимально увеличит длину циклов, этой дуги не содержащих. Таких дуг три: (1,5),(4,6),(6,2). Их запрет повышает величину нижней границы на 2. Если, например, исключить дугу (6,2), то во втором столбце матрицы длин не останется дуг нулевой длины. Минимальная по длине дуга, входящая во вторую вершину, это дуга (6,2) длины 2. Даже если все остальные дуги контура, не содержащего дугу (6,2), будут иметь нулевую длину, приведенная длина такого контура будет не менее двух, а реальная – не менее 19.
Выберем для дальнейшего ветвления, например, дугу (4,6). Длина любого контура, не содержащего дугу (4,6) не меньше 19 (рис. 4).
Таблица 4.
| j i | ||||||
| ¥ | 0(2) | |||||
| ¥ | 0(1) | |||||
|
| 0(2) | |||||
| 0(0) | 0(0) | 0(0) | ¥ | |||
| 0(0) | 0(2) | 0(0) | 0(0) | ¥ | ||
|
| 0(1) |
Оценим длины циклов, содержащих дугу (4,6). Удалим из матрицы длин четвертую строку (дуги, выходящие из четвертой вершины) и шестой столбец (другие дуги, входящие в шестую вершину). В новой матрице необходимо так же запретить дугу (6,4), чтобы исключить мини-контур 4 
6 4, проходящий через две вершины (табл. 5).
Во второй строке табл. 5 нет ни одного нуля, матрица длин приводится на 1 по второй строке (табл. 6). Значит, любой контур, содержащий дуги (3,7), (4,6) имеет приведенную длину не менее 1, а реальную – не менее .
Множество U, содержащее все 720 гамильтоновых контуров нашего графа, разбито на три непересекающихся подмножества: M 1 = {контуры, не содержащие дуги (3,7)}, r(M 1 ) =19; M2 = {контуры, содержащие дугу (3,7) и не содержащие дугу (4,6)}, r(M 2 ) =19; M 3 = {контуры, содержащие дуги (3,7) и (4,6)}, r(M 3 ) =18 (рис. 4).
Среди контуров множества M 3 может находиться контур длины 18. Среди контуров множеств M 1 и M 2 таких нет заведомо. Продолжим ветвление из вершины (4,6), соответствующей множеству M 3 с минимальной нижней границей 18 (табл. 6).
Таблица 5. Таблица 6.
| j i | ||||||
| ¥ | 0 | |||||
| ¥ | ||||||
| 0 | 0 | 0 | ¥ | |||
| 0 | 0 | 0 | ¥ | 0 | ||
|
| 0 |
| j i | |||||
| ¥ | 0(2) | ||||
| ¥ | 0(3) | ||||
| 0(0) | 0(0) | 0(0) | ¥ | ||
| 0(0) | 0(2) | 0(0) | ¥ | 0(0) | |
|
| 0(1) |
Наибольшее увеличение длин контуров дает запрет дуги (2,3) (на три
единицы). Разобьем множество M 3 на множества M 4 = {контуры, содержащие дуги (3,7), (4,6), (2,3)} и M 5 = {контуры, содержащие дуги (3,7), (4,6) и не содержащие дугу (2,3)}, r(M 5 ) =18+3=21 (рис. 4).
Найдем r(M 4 ). Включив в контур дугу (2,3), нужно удалить из табл. 6 строку 2 и столбец 3. Кроме того, нужно запретить дугу (7,2), чтобы исключить мини-контур 3-7-2-3, проходящий через три вершины (рис. 5). Новая матрица длин представлена в табл. 7.
На рис. 5 показаны три дуги, содержащиеся во всех контурах множества M 4.
В каждой строке и каждом столбце табл. 7 стоят нули, r(M 4 ) =18 (рис. 4). Продолжим поиск минимального контура среди гамильтоновых контуров множества M 4, имеющего минимальную нижнюю границу. Только среди контуров множества M 4 может оказаться контур длины 18.
Обратимся к табл. 7. Запрет дуги (1,5) увеличивает нижнюю границу длин контуров на 5. Разобьем множество M 4 на множества M 6 и M 7.
| Таблица 7 | ||||
| j i | ||||
| ¥ | 0(5) | |||
| 0(0) | 0(0) | ¥ | ||
| 0(0) | 0(2) | ¥ | 0(0) | |
| ¥ | 0(1) |
M 6 = {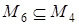 
и все контуры из множества
M 6, содержат дугу (1,5)}, M 7 = { 
и
все контуры из M7, не содержат дугу (1,5)},
r(M 7 ) =18+5=23 (рис. 4). Найдем M 6.
Удалим из табл. 7 первую строку и пятый
столбец; запретим дугу (5,1) (табл. 8). Нижняя
граница r(M 6 ) остается равной 18, во всех
строках и столбцах табл. 8 стоят нули (рис. 4). Значит, нужно разбивать множество M 6.
Таблица 8
| j i | |||
| ¥ | 0(2) | ||
| 0(4) | 0(2) | ¥ | |
| ¥ | 0(4) |
Выберем для дальнейшего ветвления,
например, дугу (6,1). Нижняя граница длин
контуров, не содержащих эту дугу равна числу
18+4=22 (рис. 4). Определим нижнюю границу
длин контуров, содержащих дугу (6,1).
Удалим из матрицы длин (табл. 8) строку 6 и столбец 1. Кроме того, нужно запретить дугу (5,4),
которая образует с уже включенными дугами (4,6), (6,1), (1,5) контур, проходящий через 4 вершины. На рис. 6 показаны 5 дуг, входящие во все контуры множества M 8 = {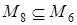 
и все контуры из M 8, содержат дугу (6,1)}.
Новая матрица дуг задана в табл. 9.
|
| |||||||||||||||||||||||||
Эта матрица доприводится по строке 5 на 2 единицы, так что r(M 8 ) =20. Приведенная матрица длин показана в табл. 10. В ней остались только две дуги нулевой длины – (5,2), (7,4).Множество M 8 содержит единственный гамильтонов контур: 
длины 20 (
).
Но гарантировать, что найденный контур минимальный, нельзя. В дереве ветвлений есть вершины, соответствующие множествам контуров с нижней границей длин, равной 19 (множества M 1 и M 2). В этих множествах могут лежать (или отсутствовать) контуры длины 19.
Перейдем ко множеству M 2 (вершина 
принадлежит более низкому ярусу, чем вершина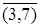 
. Это означает, что мощность множества M 2 меньше мощности множества M 1. Но чем меньше контуров во множестве, тем быстрее вычисляются нижние границы при ветвлении. Поэтому, если в дереве ветвлений присутствуют несколько висячих вершин с одинаковыми минимальными нижними границами, то ветвление нужно начинать из вершины, принадлежащей самому низкому ярусу.
Осуществим ветвление множества M 2, для чего восстановим матрицу длин, соответствующую вершине 
. Напомним, что этой вершине соответствует множество контуров, содержащих дугу (3,7) и не содержащих дугу (4,6).
Нужно восстановить табл. 4, в которой дуга (4,6) длины 0 запрещена, в клетке (4,6) стоит ¥ (табл. 11). Затем матрицу длин нужно допривести на 2 единицы по четвертой строке (табл. 12).
Таблица 11.
| j i | |||||||
| ¥ | 0 | ||||||
| ¥ | 0 | ||||||
|
| ¥ | ||||||
| 0 | 0 | 0 | ¥ | ||||
| 0 | 0 | 0 | 0 | ¥ | |||
|
| 0 |
Таблица 12.
| j i | |||||||
| ¥ | 0(2) | ||||||
| ¥ | 0(7) | ||||||
|
| 0(1) | ¥ | |||||
| 0(0) | 0(0) | 0(0) | ¥ | ||||
| 0(0) | 0(1) | 0(0) | 0(0) | ¥ | |||
|
| 0(1) |
Выберем для ветвления дугу (2,6). Длина любого контура, ее не содержащего не меньше, чем 19+7=26.
Удалим строку 2 и столбец 6 из табл. 12, запретим дугу (6,2) (табл. 13). Эта матрица длин доприводится на 1 по второму столбцу, так что длина любого цикла, содержащего дугу (2,6) не менее 19+1=20 (рис. 4).
Вывод: длина любого контура из множества M 2 не меньше 20. В этом множестве нет контуров длины 19.
Попытаемся отыскать контур длины 19 среди контуров множества M 1. Восстановим матрицу длин дуг, соответствующую множеству M 1 (табл. 14). Это просто исходная матрица длин, в которой длина дуги (3,7) равна ¥. Она доприводится на 1 по третьей строке и на 1 по седьмому столбцу (табл. 15).
Таблица 13.
| j i | |||||
| ¥ | 0 | ||||
|
| |||||
| 0 | 0 | 0 | ¥ | ||
| 0 |
| 0 | 0 | ||
|
| 0 | ||||
Таблица 14.
| j i | ||||||||
| ¥ | 0 | |||||||
| ¥ | 0 | |||||||
| ¥ | ¥ | |||||||
| ¥ | 0 | |||||||
| 0 | 0 | 0 | ¥ | |||||
| 0 | 0 | 0 | 0 | ¥ | ||||
| 0 | ¥ | |||||||
Выберем для ветвления дугу (3,6). Циклы, ее не содержащие, имеют длину не менее 24. Разрешив дугу (3,6), удалим из матрицы длин третью строку, шестой столбец и положим равной длину дуги (6,3) (табл. 16).
Матрица доприводится по второй и четвертой строкам на 3 единицы, следовательно, длина любого цикла, содержащего дугу (3,6), не менее 22 (рис. 4).
Нижние границы всех висячих вершин дерева ветвлений не меньше 20. Найденный нами контур длины 20 действительно минимален. Возможно, что в графе есть и другие контуры такой длины (во множестве M 11).
Таблица 15
| j i | |||||||
| ¥ | 0(0) | 0(0) | |||||
| ¥ | 0(1) | ||||||
| ¥ | 0(5) | ¥ | |||||
| ¥ | 0(2) | ||||||
| 0(0) | 0(0) | 0(0) | ¥ | 0(0) | |||
| 0(0) | 0(2) | 0(0) | 0(0) | ¥ | |||
| 0(1) | ¥ |
Таблица 16.
| j i | |||||||
| ¥ | 0 | ||||||
| ¥ | |||||||
| ¥ | |||||||
| 0 | 0 | 0 | ¥ | ||||
| 0 | 0 | ¥ | 0 | ||||
| 0 | ¥ |
Исходное множество 
, содержащее все 720 гамильтоновых контуров, разбито на 8 непересекающихся подмножеств:
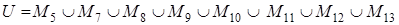(рис. 4)
Например, M 11 = {множество контуров, содержащих дуги (3,7) и (2,6) и не содержащих дугу (4,6)}; M 9 = {множество контуров, содержащих дуги (4,6), (2,3),(1,5) и не содержащих дугу (6,1)}; M 8 = {контур минимальной длины 20} и т. д.
Дата добавления: 2015-08-27; просмотров: 102 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача коммивояжера и ее решение методом ветвей и границ | | | Цель занятия. |