Основні теореми про границі

1. Якщо функція y = f (x) у точці x ₀ має границю, то ця границя єдина.

2. Якщо в точці х ₀ існують скінченні границі функцій f і g (, 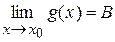), то в цій точці існують також скінченні границі функцій: f + g, f – g, f × g, 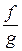(остання границя буде скінченною за умови 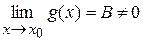), причому:

а) ;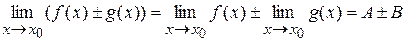

б) ;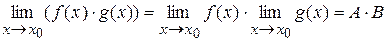

в) .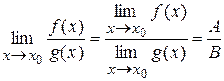

3. Якщо 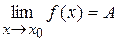(А ¹0), а , то .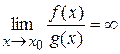

4. Якщо 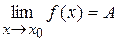(А – скінченне число), а 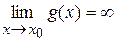, то .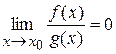

При знаходженні границь часто використовують деякі важливі границі, наведені нижче.

1. 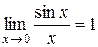(перша чудова границя).

1.1. .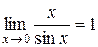

2. 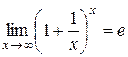або 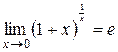(друга чудова границя).

3. .

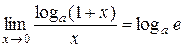3.1. .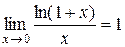

4. .

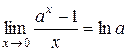4.1. .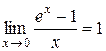

5. 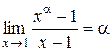або .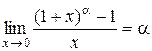

Якщо 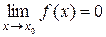то функцію f називають нескінченно малою в точці х ₀. Якщо 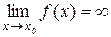то функцію f називають нескінченно великою в точці х ₀.

Нескінченно малі (нескінченно великі) у точці х ₀ функції f і g називають еквівалентними, якщо 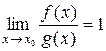. При цьому записують ~ , .

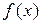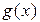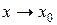Ураховуючи важливі границі, маємо такі еквівалентності при :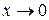

, , ,

, , .

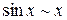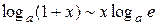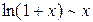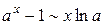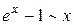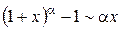При знаходженні границі 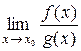нескінченно малі (нескінченно великі) функції f і g можна замінювати еквівалентними функціями f ₁ і g ₁, тобто 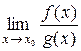= 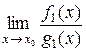, якщо 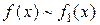, 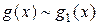при .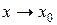

Дата добавления: 2015-08-26