
|
Читайте также: |
1. Користуючись означенням границі функції в точці, знайти границі:
а)  ; б)
; б)  .
.
Розв’язання. а) Розглянемо довільну послідовність (xn), що володіє властивостями:
1) xn ¹3 " n Î N і 2)  =3
=3
(оскільки функція 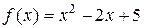 визначена на всій числовій прямій, а, отже, і в будь-якому околі точки 3, то умова xn ÎО(3) " n Î N не накладається). Враховуючи, що
визначена на всій числовій прямій, а, отже, і в будь-якому околі точки 3, то умова xn ÎО(3) " n Î N не накладається). Враховуючи, що 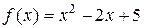 , за властивостями границь послідовностей маємо
, за властивостями границь послідовностей маємо
 =
=  =
=  =32–2×3+5=8.
=32–2×3+5=8.
Отже, за означенням границі функції в точці  .
.
б) Нехай (xn) – довільна послідовність, що володіє властивостями:
1) xn ¹–5 " n Î N і 2)  =–5
=–5
(оскільки функція  визначена на всій числовій прямій, окрім точки –5, а, отже, в будь-якому проколеному околі точки –5, то умова xn ÎО(–5) " n Î N не накладається).
визначена на всій числовій прямій, окрім точки –5, а, отже, в будь-якому проколеному околі точки –5, то умова xn ÎО(–5) " n Î N не накладається).
Знайдемо  . Якщо xn ®–5 (n ®¥), то чисельник і знаменник дробу
. Якщо xn ®–5 (n ®¥), то чисельник і знаменник дробу 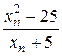 прямують до нуля. Тому застосовувати властивість про границю частки послідовностей не можна. Але оскільки xn ¹–5 " n Î N, то даний дріб можна скоротити на xn +5, а потім знайти границю:
прямують до нуля. Тому застосовувати властивість про границю частки послідовностей не можна. Але оскільки xn ¹–5 " n Î N, то даний дріб можна скоротити на xn +5, а потім знайти границю:
 =
=  =
=  =
=  =–5–5=–10.
=–5–5=–10.
Отже, за означенням границі функції в точці  =–10.
=–10.
2. Довести, що функція  у точці х 0=0 не має границі (рис.3.20).
у точці х 0=0 не має границі (рис.3.20).
Розв’язання. Розглянемо послідовність (xn), що збігається до х 0=0:
xn =  , n =1, 2, 3, ….
, n =1, 2, 3, ….
Оскільки xn =  >0 " n Î N, то f (xn)=1 " n Î N і тому
>0 " n Î N, то f (xn)=1 " n Î N і тому  =
=  =1.
=1.
 Розглянемо тепер іншу послідовність (
Розглянемо тепер іншу послідовність ( ), що збігається до х 0=0:
), що збігається до х 0=0:
 =–
=–  , n =1, 2, 3, ….
, n =1, 2, 3, ….
Оскільки  =–
=–  <0 " n Î N, то f (
<0 " n Î N, то f (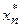 )=–1 " n Î N і тому
)=–1 " n Î N і тому  =
=  =–1.
=–1.
Отже, для двох різних послідовностей (xn) і ( ), що збігаються до точки х 0=0, маємо
), що збігаються до точки х 0=0, маємо  ¹
¹  . А це означає, що функція f (x)=sign x в точці х 0=0 не має границі.
. А це означає, що функція f (x)=sign x в точці х 0=0 не має границі.
3. Знайти границі:
а) 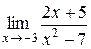 ; б)
; б)  ; в)
; в)  ; г)
; г) 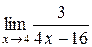 ;
;
д)  ; е)
; е)  ; є)
; є)  ;
;
ж)  ; з)
; з)  ; и)
; и)  .
.
Розв’язання. а) Використовуючи теореми про границю суми і границю добутку функцій, знайдемо границі чисельника і знаменника дробу:
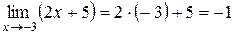 ,
, 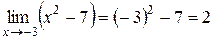 .
.
Оскільки знайдені границі є скінченними і границя знаменника не дорівнює нулю, то за теоремою про границю частки маємо:
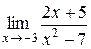 =
=  .
.
б) Знайдемо границі чисельника і знаменника:
 ,
,  .
.
Оскільки границі чисельника і знаменника дорівнюють нуля при х ®2, то використовувати теорему про границю частки не можна. У цьому випадку маємо невизначеність вигляду  . Щоб її усунути, спочатку розкладемо вираз у чисельнику на лінійні множники, використавши формулу скороченого множення
. Щоб її усунути, спочатку розкладемо вираз у чисельнику на лінійні множники, використавши формулу скороченого множення  :
:
 .
.
Розкладемо квадратний тричлен у знаменнику на лінійні множники, використавши формулу  , де х 1, х 2 – корені тричлена;
, де х 1, х 2 – корені тричлена;
 .
.
Далі скоротимо дріб на вираз  . Таке скорочення можливе, оскільки цей вираз не дорівнює нулю (адже за означенням границі функції в точці маємо, що х»2, але х ¹2). Отже,
. Таке скорочення можливе, оскільки цей вираз не дорівнює нулю (адже за означенням границі функції в точці маємо, що х»2, але х ¹2). Отже,
 =
=  =
=  =
=  .
.
в) Якщо х ®5, то границі чисельника і знаменника дорівнюють нулю:
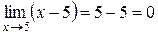 ;
;  .
.
Отже, маємо невизначеність вигляду  . Помноживши чисельник і знаменник на спряжений до знаменника вираз
. Помноживши чисельник і знаменник на спряжений до знаменника вираз  і після перетворень скоротивши дріб на
і після перетворень скоротивши дріб на  , одержимо:
, одержимо:
 =
=  =
=  =
=
=  =
=  =
= 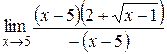 =
=
=  .
.
г) Оскільки при х ®4 границя чисельника є відмінне від нуля число 3, а границя знаменника дорівнює нулю, то за теоремою 3 маємо:
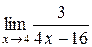 =¥.
=¥.
д) Оскільки  і
і  , то маємо невизначеність вигляду
, то маємо невизначеність вигляду  . Щоб її усунути поділимо чисельник і знаменник дробу на х 4, а потім скористаємося теоремою про границю частки:
. Щоб її усунути поділимо чисельник і знаменник дробу на х 4, а потім скористаємося теоремою про границю частки:
 =
= 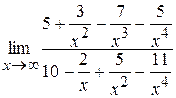 =
=
= 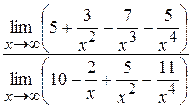 =
=  =
=  .
.
е) Якщо х ®0, то 4 х ®0 і sin5 х ®0. Тому маємо невизначеність вигляду  . Для знаходження
. Для знаходження  скористаємося першою чудовою границею
скористаємося першою чудовою границею  =1:
=1:
 =
=  =
=  .
.
Можна знайти задану границю простіше, скориставшись еквівалентністю нескінченно малих функцій. Оскільки  , х ®0, то
, х ®0, то
 =
= 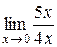 =
= 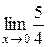 =
=  .
.
є) Якщо х ®0, то sin4 х ®0 і tg3 х ®0. Тому також маємо невизначеність вигляду  . Для знаходження
. Для знаходження  скористаємося границями:
скористаємося границями:  =1,
=1,  =1 та врахуємо, що сos3 x ®1, коли х ®0:
=1 та врахуємо, що сos3 x ®1, коли х ®0:
 =
=  =
= 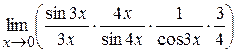 =
=
=  =
=  .
.
ж) Якщо х ®¥, то 4 х –1®¥ і 4 х +2®¥. Тому, знаходячи  , маємо невизначеність вигляду
, маємо невизначеність вигляду  . Поділивши чисельник і знаменник дробу
. Поділивши чисельник і знаменник дробу  на х, знайдемо границю:
на х, знайдемо границю:  =
=  =
=  . Якщо х ®¥, то 4 х –3®¥. Отже, обчислюючи границю
. Якщо х ®¥, то 4 х –3®¥. Отже, обчислюючи границю  , маємо невизначеність вигляду 1¥. Щоб її усунути використаємо другу чудову границю
, маємо невизначеність вигляду 1¥. Щоб її усунути використаємо другу чудову границю  . Для цього перетворимо вираз
. Для цього перетворимо вираз  так, щоб він містив вираз вигляду
так, щоб він містив вираз вигляду  :
:
 =
= 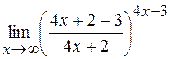 =
= 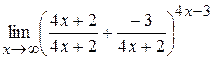 =
=
= 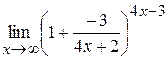 =
=  =
=
=  =
=  .
.
Останню границю знайдемо як границю степеня. Для цього знайдемо границю основи степеня  і границю показника степеня
і границю показника степеня  при х ®¥. Оскільки вираз
при х ®¥. Оскільки вираз  має вигляд
має вигляд  , причому
, причому  , коли х ®¥, то
, коли х ®¥, то  . Отже, маємо:
. Отже, маємо:
 =
=  =
=  =
= 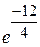 =
=  =
=  .
.
з) Якщо х ®4, то 2 х –7®1, х –4®0,  ®¥. Отже, знаходячи границю
®¥. Отже, знаходячи границю  , маємо невизначеність вигляду 1¥. Щоб її усунути використаємо другу чудову границю
, маємо невизначеність вигляду 1¥. Щоб її усунути використаємо другу чудову границю  .
.
Оскільки х ®4, то х –4®0. Тому  =
=  . Введемо заміну: х –4= y. Тоді х = y +4, 2 х =2 y +8, 2 х –7=2 y +1. Враховуючи заміну, маємо:
. Введемо заміну: х –4= y. Тоді х = y +4, 2 х =2 y +8, 2 х –7=2 y +1. Враховуючи заміну, маємо:  =
=  =
=  .
.
Оскільки вираз  має вигляд
має вигляд  , причому
, причому 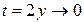 , коли y ®0, то
, коли y ®0, то  . Отже, остаточно маємо:
. Отже, остаточно маємо:
 = e 6.
= e 6.
и) Оскільки  і
і  , то маємо невизначеність вигляду
, то маємо невизначеність вигляду  . Перетворивши дріб і скориставшись важливими границями
. Перетворивши дріб і скориставшись важливими границями 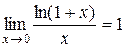 ,
,  ,
,  =1, одержимо:
=1, одержимо:
 =
= 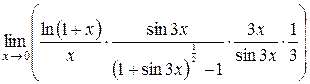 =
=  .
.
4. Знайти ліву і праву границі функції f у точці х 0:
а)  , х 0=2; б)
, х 0=2; б)  , х 0=–3.
, х 0=–3.
Розв’язання. а) Знаходячи ліву границю функції f у точці х 0=2, вважають що х ®2 і х <2. Тому
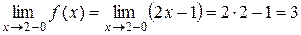 .
.
При знаходженні правої границі функції f у точці х 0=2, вважають що х ®2 і х >2. Тому
 .
.
Оскільки ліва і права границі функції f у точці х 0=2 дорівнюють одна одній, то існує  .
.
б) Якщо х ®–3 і х <–3, то чисельник дробу прямує до від’ємного числа –6 (2 х ®–6), а знаменник є нескінченно малою від’ємною функцією (х +3®0 і х +3<0). Тому  .
.
Якщо х ®–3 і х >–3, то чисельник дробу прямує до від’ємного числа –6 (2 х ®–6), а знаменник є нескінченно малою додатною функцією (х +3®0 і х +3>0). Тому  .
.
Завдання для самостійного розв’язування
12. Користуючись означенням границі функції в точці, знайти границі:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
13. Знайти границі:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7) 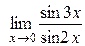 ;
;
8) 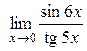 ; 9)
; 9) 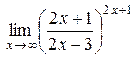 ; 10)
; 10)  ;
;
11)  .
.
14. Знайти односторонні границі функції f у точці х 0:
а)  , х 0=0; б)
, х 0=0; б)  , х 0=–5;
, х 0=–5;
в)  , х 0=0; г)
, х 0=0; г)  , х 0=1.
, х 0=1.
Відповіді:
12. а) –3; б)  ; в) 0; г) ¥.
; в) 0; г) ¥.
13. 1) –13; 2) –5; 3) 3; 4) 6; 5) ¥; 6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  ; 11) 2.
; 11) 2.
14. а)  ,
,  ; б)
; б)  ,
,  ; в)
; в) 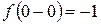 ,
,  ; г)
; г)  ,
, 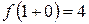 .
.
Дата добавления: 2015-08-26; просмотров: 86 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основні теореми про границі | | | ЧАСТЬ ПЕРВАЯ |