
Читайте также:
|


 M1M/ MM2,λ-заданное число
M1M/ MM2,λ-заданное число
 M1M=
M1M= 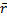 -
- 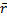 1
1
 MM2=
MM2= 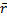 2-
2- 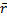

 M1M=λ* MM2→
M1M=λ* MM2→ 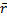 -
- 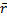 1=λ*(
1=λ*(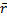 2-
2- 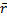 )→(1+λ)*
)→(1+λ)* 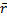 =
= 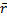 1+λ*
1+λ* 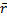 2→
2→ 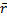 =(
=(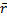 1+ λ*
1+ λ* 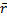 2)/ (1+λ)
2)/ (1+λ)
Рассмотрим для осей x, y, z
x=(x1+λ*x2)/ (1+λ)
y=(y1+λ*y2)/ (1+λ)
z=(z1+λ*z2)/ (1+λ)
Для медианы λ=1→ x=(x1+x2)/2; y=(y1+y2)/ 2; z=(z1+z2)/ 2;
Для центра (пересечение медиан) λ=2→ x=(x1+2*x2)/3;y=(y1+2*y2)/ 3; z=(z1+2*z2)/ 3
Скалярное произведение векторов называется число равное произведению длин этих векторов на косинус угла между ними  *
*  =
=  *
*  *
*  , свойства:
, свойства:
1) ( *
*  )=(
)=( *
*  )
)
2) ( *
*  )=
)= 
3) Скалярное произведение равно нулю, когда один из векторов равен нулю, либо вектора перпендикулярны
4)  *(
*( +
+ 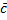 )=
)=  *
*  +
+  *
* 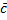
5) λ*( *
*  =(λ*
=(λ*  )*(
)*( *λ)
*λ)
6) (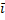 *
* 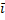 )=(
)=( *
*  )=(
)=( *
*  )=1
)=1
(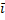 *
*  )=(
)=( *
*  )=(
)=( *
* 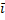 )=0
)=0
7) 


 ax; ay; az ;
ax; ay; az ;  bx; by; bz
bx; by; bz
 *
*  = ax*bx+ay*bz +by*bz вывод формулы:
= ax*bx+ay*bz +by*bz вывод формулы:
 *
*  =(
=( x*
x* 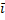 +
+  y*
y*  +
+  z*
z*  )*(
)*( x*
x* 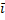 +
+  y*
y*  +
+  z*
z*  )=
)=  x*
x*  x(
x(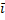 *
* 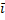 )+ay*
)+ay*  y
y  *
* 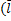 *
*  )=az*
)=az*  z*(
z*( *
*  )= ax*bx+ay*bz +by*bz
)= ax*bx+ay*bz +by*bz
Вывод формулы угла:  *
*  =
=  *
*  *
*  ;
;  *
*  = ax*bx+ay*bz +by*bz
= ax*bx+ay*bz +by*bz
 = (ax*bx+ay*bz +by*bz)/
= (ax*bx+ay*bz +by*bz)/  *
*  =
=  *
*  /
/  *
* 
 и
и  вектора произведения, обладающие следующим вектором -
вектора произведения, обладающие следующим вектором - 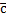
Свойства:
1) 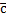 ┴
┴  ,
, 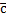 ┴
┴  ;
;
2) 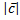 =
=  *
*  *
* 

 /
/ 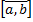 , свойства:
, свойства:
1) 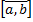 =-
=- 
2)  *(
*( +
+ 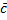 )=
)=  *
*  +
+  *
* 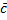
3) λ* 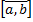 =
= 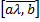 =
= 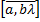
4) 
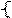
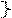

 ax; ay; az ;
ax; ay; az ;  bx; by; bz
bx; by; bz

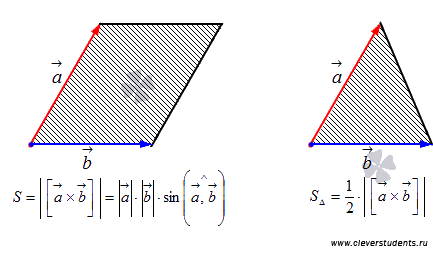
Площадь параллелограмма:


Отсюда можно найти S▲=  SABCD
SABCD
Смешанное произведение векторов. Смешанным (векторно-скалярным) произведением векторов  ,
,  ,
,  называется число, определяемое по формуле:
называется число, определяемое по формуле:  =(
=( ×
×  )*
)*  =
=  *(
*( ×
×  )
)
Свойства смешанного произведения:
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т.е.  =
=  =
=  .
.
2. При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный, т.е.  =
=  =
=  =-
=-  .
.
3. Необходимое и достаточное условие компланарности трех векторов  ,
,  ,
,  :
:  =0.
=0.
4. Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е.  = + V.
= + V.
Если известны координаты векторов  (ax; ay; az),
(ax; ay; az),  (bx; by; bz),
(bx; by; bz), 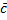 (cx; cy; cz), то смешанное произведение находится по формуле:
(cx; cy; cz), то смешанное произведение находится по формуле:

Дата добавления: 2015-08-27; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Проекция вектора на ось | | | Кантонская ярмарка 2014 (Осень) |