
Читайте также:
|


Прx  =
=  x=
x=  *
*  (1)
(1)
Прy  =
=  y=
y=  *
*  (2)
(2)
Прz  =
=  z=
z=  *
*  (3), если есть z
(3), если есть z

 Координатами вектора называются проекции вектора на координатные оси
Координатами вектора называются проекции вектора на координатные оси
A (x1, y1, z1), B(x2, y2, z2), тогда  x2-x1; y2-y1; z2-z1
x2-x1; y2-y1; z2-z1



 ax; ay; az, тогда длинна вектора равна
ax; ay; az, тогда длинна вектора равна 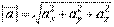
Расстояние между двумя точками  =
= 
Разложение вектора по базису  =
=  x*
x* 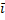 +
+  y*
y*  +
+  z*
z* 
Основные теоремы о проекциях:


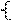 Теорема1. При сложении двух векторов их координаты складываются
Теорема1. При сложении двух векторов их координаты складываются
 ax; ay; az ;
ax; ay; az ;  bx; by; bz
bx; by; bz
 =
=  x*
x* 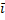 +
+  y*
y*  +
+  z*
z*  ;
;  =
=  x*
x* 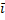 +
+  y*
y*  +
+  z*
z* 
( +
+  )=
)=  x*
x* 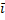 +
+  y*
y*  +
+  z*
z*  +
+  x*
x* 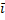 +
+  y*
y*  +
+  z*
z*  = (
= ( x +
x +  x)*
x)* 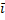 +(
+( y+
y+  y)*
y)*  +(
+( z+
z+  z)*
z)* 


 +
+  =
=  x +
x +  x;
x;  y+
y+  y;
y;  z+
z+  z
z
Теорема2. При умножении вектора на число λ координаты вектора тоже умножаются на это число
λ*  =λ*(
=λ*( x*
x* 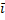 +
+  y*
y*  +
+  z*
z*  )=(λ*
)=(λ*  x)*
x)* 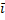 +(λ*
+(λ*  y)*
y)*  +(λ*
+(λ*  z)*
z)* 

 λ*
λ*  λ*
λ*  x; λ*
x; λ*  y; λ*
y; λ*  z
z
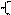
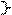 Теорема 3. Если даны две точки M1(x1;y1;z1) и M2(x2; y2; z2), то
Теорема 3. Если даны две точки M1(x1;y1;z1) и M2(x2; y2; z2), то 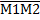 x2-x1; y2-y1; z2-z1
x2-x1; y2-y1; z2-z1

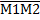 =
= 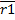 -
-  =x2*
=x2* 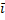 + y2*
+ y2*  +z2*
+z2*  -x1*
-x1* 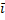 +y1*
+y1*  +z1*
+z1*  = (x2-x1)*
= (x2-x1)*  (y2-y1)*
(y2-y1)*  +(z2-z1)*
+(z2-z1)* 
Условие коллинеарности векторов(из 2-й теоремы):


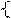

 ax; ay; az;
ax; ay; az;  bx; by; bz, векторы коллинеарны, если
bx; by; bz, векторы коллинеарны, если  =λ*
=λ*  (λ≠0)
(λ≠0)
Тогда  x=λ*
x=λ*  x,
x,  y=λ*
y=λ*  y,
y,  z=λ*
z=λ*  z, следовательно λ=ax/bx=ay/by= az/bz
z, следовательно λ=ax/bx=ay/by= az/bz
 ||
||  , если
, если  противоположен
противоположен 
Дата добавления: 2015-08-27; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Материал: лен / хлопок / шелк | | | Деление отрезков в заданном отношении |